On Becoming Unstuck

I haven’t written an editorial. I was stuck for ideas. Instead, I let my mind wander and once all the news of impending doom, jobs to do around the house, talks to prepare and the like bubbled up and got added to a to-do list, I was tempted to wander off myself. I did spend some time collecting all my hand scribbled to-do lists and putting them in once place. I should probably make a new list and throw out the old ones. I’ll play today’s Wordle first though – little rituals to make yourself sit still long enough to start concentrating can be very important. Playing some music works too. If I play a whole album rather than leave random play on, I can persuade myself to sit at my desk for the duration of the music and thereby manage to get stuff done too. Good music, goal accomplished: win, win.

It’s not always that easy though, and the stuff I get done may not be what I first intended. Distractions abound when you don’t have a clear goal in mind, can’t form your list into a priority queue, or worse find the list is more like a tree structure with each thing you think of kicking off twice as many extra things to deal with. You may have heard of Feynman’s algorithm, “facetiously suggested by Murray Gell-Mann, a colleague of Feynman, in a New York Times interview” [c2.com14]:

1. Write down the problem.
2. Think very hard.
3. Write down the solution.

On the face of it, the suggestion seems trite and unhelpful. Furthermore, some suggest that the algorithm only works if you are Feynman himself. Variations on the same idea have been suggested, for example from Hacker News [Hacker]:

1. Write down the problem.
2. Try several established strategies to solve it.
3. Get stuck, resign self to failing.
4. Go to sleep.
5. Write out the answer over breakfast.

Aside from the apparent frivolity, trying to write down a problem often helps one to focus on a specific goal. Like talking to the fabled rubber duck to debug an issue, trying to be clear about what you are stuck on might help you get unstuck. I say ‘unstuck’; I am aware that ‘coming unstuck’ can also mean everything falling apart and failing, but let’s stay positive and stick to problem solving instead of doom-scrolling.

Stepping away from the keyboard and doing something else halts doom surfing, and likewise many problems can be solved by doing something completely different, though this may get mislabelled as work avoidance by the doubters. I once decided it was far more important to wash the skirting boards than revise for a looming exam. Some friends at university tried to ‘mow’ the lawn with nail scissors. We’ve all been there. Eventually, you have to face whatever it is you were supposed to be doing. I suspect changing from sitting down staring at a book or screen and physically moving shifts your perspective. Going for a walk or getting some other form of exercise can clear your head too. It might be because you are still thinking on the problems or issues while doing a menial task, but can’t keep digging down deeper in the hole you started, making more notes and ending up with an exponential number of problems. If you can’t just get up and go for a walk, because you are stuck in an office – remember those days? – or in an exam or similar, try a different problem. If you’re stuck on one question, try another one and revisit the first one later. In a similar vein, George Polya once said “If you can't solve a problem, then there is an easier problem you can solve: find it” [Polya73]. This advice was aimed at solving mathematical problems. To solve an equation, guess a value and see if it works. In the process you might notice ways to eliminate some terms or similar. Resorting to solving a simpler problem helps too. If you are trying to integrate something messy looking, substituting a variable might work. This can be a bit like extracting a method when you refactor – leaving less cognitive load by breaking up complicated ideas. Flushing out edge cases and impossibilities leaves less to think through as well. Similar tricks work when programming, though don’t forget, “We can solve any problem by introducing an extra level of indirection, except for the problem of too many levels of indirection” [Wikipedia-1]. If you can’t figure out an algorithm using a tree structure, maybe try an array first. With one item in. Or, even none. Sometimes tidying up code, or writing some documentation, or deleting code helps shift your focus enough to go back and tackle the initial problem. “A change is as good as a rest”, as the saying goes.

Polya’s advice was aimed at getting students themselves to form a plan to tackle problems rather than the teacher giving step by step instructions. This helps students to actually learn. Solving a different problem that is similar frequently hints at ways forward and noticing connections like these shows knowledge is growing. An extreme version of solving a different problem would be coming out with Plan B if Plan A doesn’t work. It is hard to know when to abandon hours of work and try something else, since the alternative may not work either. Nonetheless, the different perspective might suggest a way forward for the first attempt. You won’t know until you try. If neither plan works, resort to moving the goal posts. This might mean scratching some items off a to-do list or asking a customer if some feature can wait for another day. If you get stuck solving one problem, give up and solve a different one.

Some problems are hard. In fact some problems, such as the halting problem are NP-hard. In case you have forgotten the definition:

A problem is NP-hard if an algorithm for solving it can be translated into one for solving any NP-problem (nondeterministic polynomial time) problem. NP-hard therefore means ‘at least as hard as any NP-problem’, although it might, in fact, be harder. [Wolfram]

If that didn’t help much, the salient point here is some problems can be reduced to other problems, which you could try to solve instead. If you can’t solve the problem and someone else offers a solution, you might be able to verify it works. Perhaps the main lesson from the P=NP question, and also Feynman’s algorithm, is to delegate to someone else.

If you can’t move the target or abandon requirements and have a mammoth task in front of you which you can’t delegate, start with the first step. One thing at a time. It’s not always obvious where to start though. A large task, like preparing a conference talk or writing a book can be daunting. So, where do you start? Truth be told, usually in the middle. From the outside, a title and table of contents may appear to be produced first, however some thoughts or sketchy notes for a few important ideas that fit somewhere, exactly where to be decided, usually come first. Maybe start with a few tests, then make a to-do list? Maybe draw a mock up on a white board? Perhaps read up on the state-of-the-art – a very important part of research. We can’t all spend our time reinventing the wheel. As you read around a subject you may find someone else has already solved your problem. Job done. Unfortunately, you may Google a problem and find you’ve asked the exact same question years ago on a forum somewhere. And still no one knows the answer. That’s possibly a good thing. Sit back, relax and cherish having something difficult to think about. Take a deep breath and have another go.

Some problems do have known solutions, but you can still get stuck when you apply them. For example, some techniques for root finding [Martin16] require an initial guess which gets updated in a loop. Annoyingly, the algorithm can head to other roots, go to infinity, or get trapped in cycles. In order to find where a function, f, has the value zero, also known as root finding, you can start with an initial guess of x₀ and find a better approximation x₁ by calculating

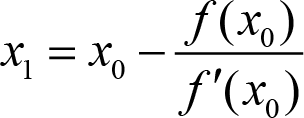
where fʹ is the derivative of f. Then reapply the formula to the new approximation and keep going. If you can’t find the derivative, you’re slightly stuck, but could try to calculate that numerically. Once you have fʹ, you might end up with a division by zero problem. Also, a bad initial guess can get you in trouble too. [Wikipedia-2]. You might have to think carefully about where to start before applying this and similar techniques. As a saying goes, “If I wanted to get there, I wouldn’t start from here.” At the very least, if you are tempted to have code in a while loop waiting for a condition to be met, consider dropping out after a pre-specified number of iterations so you don’t loop forever. Instead of iterating, some algorithms rely on recursion. Instead of getting stuck in a loop, you are likely to hit a stack overflow at some point if your stopping condition is wrong. You may not be stuck, but you certainly haven’t solved your problem.

There are many ways to get stuck and many things to get stuck on. Patricia Aas recently asked the world what the longest time people had spent debugging an issue was and how big the fix was [Aas22]. As you can imagine, there were many replies. My favourite was someone spending a day debugging an I/O issue until a colleague pointed out the network cable was unplugged. I confessed to having spent several days looking at a networking issue for some low-level embedded devices. I even spent hours looking at the output on a protocol analyser. Eventually the presence of a \n character came into focus. The nice small fix was to change it to a \r. Many problems in IT are hard to spot, but when you find them you might only need one small change to sort things out. That might seem as unhelpful as Feynman’s algorithm, but reminding myself the issue is probably something small, simple and obvious, even though I haven’t found it yet can help me avoid panicking and start being more systematic about how to troubleshoot.

Having the wrong line ending character was my fault and quickly fixed; however, sometimes things beyond your control cause problems. We’re having our house rewired; annoying but necessary. This gave us the opportunity to put in a network cable because Wi-Fi doesn’t always work very well through old stone walls. You’ll never guess what happened next. Well, you might. The internet stopped working. The new cable was to connect the main router to another in the office, so had no reason to stop the internet into the house. We couldn’t fix it so had to phone our internet provider’s help line. It ‘magically’ started working again during the course of the call. Interesting. We were using our own router, so they decided to send us one of theirs in case it happens again. This time you really won’t guess what happened next. I discovered a package, yep the new router, literally stuck in the letterbox. I guess the posty had tried to shove it through the letterbox, failed, couldn’t get it back out and ran away. It needed two of us to hold the letter box open and force the parcel back out. If something is about to get stuck, maybe give up and summon help? Just saying.

References

[Aas22] Patricia Aas, on Twitter: https://twitter.com/pati_gallardo/status/1499517651999420416

[c2.com14] The Feynman Algorithm: http://wiki.c2.com/?FeynmanAlgorithm (page last updated December 2014)

[Hacker] Hacker News: https://news.ycombinator.com/item?id=14191681

[Martin16] Patrick Martin, ‘Eight Rooty Pieces’, Overload, 24(135):8-12, October 2016. https://accu.org/journals/overload/24/135/martin_2294/

[Polya73] George Polya, How to Solve It: A New Aspect of Mathematical Method. Princeton University Press, 1973. See also https://en.wikipedia.org/wiki/How_to_Solve_It

[Wikipedia-1] Fundamental theorem of software engineering: https://en.wikipedia.org/wiki/Fundamental_theorem_of_software_engineering

[Wikipedia-2] Newton’s method: https://en.wikipedia.org/wiki/Newton%27s_method#Failure_of_the_method_to_converge_to_the_root

[Wolfram] NP-Hard Problem, Wolfram Mathworld, athttps://mathworld.wolfram.com/NP-HardProblem.html#:~:text=A%20problem%20is%20NP%2Dhard,%2C%20in%20fact%2C%20be%20harder

Frances Buontempo has a BA in Maths + Philosophy, an MSc in Pure Maths and a PhD technically in Chemical Engineering, but mainly programming and learning about AI and data mining. She has been a programmer since the 90s, and learnt to program by reading the manual for her Dad’s BBC model B machine.