Concurrency can be hard to get right. Lucian Radu Teodorescu demonstrates how tasks can help.
Probably the most important method that we apply when designing software is decomposition; this comes in the same package as composition. All the rest are irrelevant if we cannot decompose software. Even the highly acclaimed abstraction is insignificant compared to this pair.
Indeed, if we cannot decompose the system into multiple independent parts, then we could only apply the abstraction to the whole software. Thus, we would have the whole system and the abstracted whole system. There would be no other part that could benefit from using the abstraction instead of the whole system. So, the abstraction would be completely useless.
When one needs to solve a complex problem, one applies decomposition to break that problem into multiple parts that are easier to conceive, understand and develop. Thus, a software system is decomposed into multiple subsystems/components. I cannot think of any software system, even the most simple ones, that cannot be decomposed into simpler systems. That’s just how our world is.
Ideally, the subsystems of a system can be developed in parallel, at least to a certain degree. Then, it’s important that those subsystems can be put together, so that we can form the whole system.
Let’s take a simple example, using functional decomposition and composition. Let’s assume that for a given number n we want to compute f(n) = n2 + 1. To solve this problem, we can decompose it in two smaller sub-problems: square a number, and add 1 to a number. That is, we reduce the initial problem to solving two other problems: computing sqr(n) = n2 and inc(n) = n + 1. After implementing these smaller functions, we need to combine them in the following way: f(n) = inc (sqr (n) ), or, more commonly in mathematics: f = inc ∘ sqr.
Decomposition and composition are the two faces of the same coin. One is useless without the other. For example, it’s useless to decompose a software system into multiple components, if we can’t compose the smaller components to form the larger system. They are so tied together that I cannot resist the urge to quote Heraclitus:
The road up and the road down is one and the same.
This article aims to show that by using tasks, one can achieve good decomposability and composability, and thus tasks can be used as building blocks for concurrency.
Threads and locks are not composable
We all know that programming using raw threads and locks (in general, synchronisation primitives) is hard. We have understandability problems, we have thread safety problems, and most often we have performance problems. But one important inconvenience of this concurrent programming style is that raw threads and locks are not composable. [Lee06]
To ensure proper functioning of a subcomponent, one needs to understand the threading constraints of the adjacent subcomponents; that is, from what threads the subcomponent will be called, and what are the locks that are held while making these calls.
If one component holds a lock while calling the other, we need to be very sure that the other component will not call the first component back in a call that would require the same lock. And we need to make sure we are always taking all the locks in the same order, even if we don’t have visibility of the other components. Also, components cannot assume that some APIs will be called from a known set of threads; a component will never know the threading used by adjacent components.
There are ways to protect against these types of safety problems, but they typically fall into two categories:
- They are not general enough to be applied to all types of problems (i.e., they are ad hoc).
- They typically degrade overall performance (they involve adding locks and restrictions).
To better illustrate this, let’s revisit the simple example that Edward Lee used [Lee06]. Consider a single-threaded implementation of the observer pattern, as shown in Listing 1. If this is run inside a component that only calls addListener and setValue from a single thread, then this would be ok. But if another component tries to call this from a different thread, then we have a potential race condition; and, it’s somehow normal to expect other components to maybe call this from different threads.
template <typename T>
class ValueHolder {
public:
using Listener = std::function<void(T)>;
void addListener(Listener listener) {
listeners_.push_back(std::move(listener));
}
void setValue(T newVal) {
curValue_ = std::move(newVal);
for ( lstner : listeners_ )
lstner(curValue_);
}
private:
std::vector<Listener> listeners_;
T curValue_;
};
|
| Listing 1 |
To fix this, one would add locks around the critical code, something similar to what is shown in Listing 2. This may work in certain cases, but not in others; depending on how listeners are implemented, this can lead to a deadlock. In general, it is bad practice to call unknown functions while holding a lock.
template <typename T>
class ValueHolder {
public:
using Listener = std::function<void(T)>;
void addListener(Listener listener) {
std::unique_lock<std::mutex> lock{bottleneck_};
listeners_.push_back(std::move(listener));
}
void setValue(T newVal) {
std::unique_lock<std::mutex> lock{bottleneck_};
curValue_ = std::move(newVal);
for ( lstner : listeners_ )
lstner(curValue_);
}
private:
std::vector<Listener> listeners_;
T curValue_;
std::mutex bottleneck_;
// Yes, this is a bottleneck
};
|
| Listing 2 |
Another potential fix may be to extract the calling of the listeners from the lock, as shown in Listing 3. Now, even this version may have some problems, but in general, most people would agree that this is a good solution.
void setValue(T newVal) {
std::vector<Listener> listenersCopy;
{
std::unique_lock<std::mutex> lock{bottleneck_};
curValue_ = std::move(newVal);
listenersCopy = listeners_;
}
for ( lstner : listenersCopy )
lstner(curValue_);
}
|
| Listing 3 |
If one can draw the conclusion that, in a threads and locks approach, to be able to interoperate with other components, one needs to encapsulate the threading behaviour, hardening the threading assumptions. In general, cross-API calls need to be made without holding any lock, and all the incoming calls need to be assumed that can be coming from any thread.
This is a simple example. The problems can only amplify for larger and more complex systems.
The composition for threads and locks systems is ad hoc, with effort needed to prevent safety issues, and, in general, with performance issues. It is hard to obtain good composability within systems based on threads and locks.
Decomposition with threads and locks
Decomposition is seldom associated with threads and locks. This is mainly because there are no general rules for decomposition.
One can speak of decomposition when separating out complex processes into multiple threads. But, each time we do that, we encounter the two usual problems: safety and performance. To solve the safety problem, we typically need to add more locks. As we know, adding more locks typically downgrades performance.
There is also another performance problem caused by too many threads. One cannot simply create numerous threads if one has a limited number of cores. Assuming CPU-intensive work, the optimal performance is obtained when the number of threads is equal to the number of cores. Thus, decomposing in terms of threads seems like a bad idea.
Bottom line, decomposition with threads and locks is, at best, ad hoc.
Composability of task systems
Compared to the classical threads and locks approach, task-based systems compose better. The composability advantages of tasks systems can be summarised as follows:
- no extra protection needed at the interface level (i.e., adding a component to an existing component does not compromise its safety)
- no safety issue
- no loss in performance
We will analyse all these point one at a time, but before doing that let’s introduce some formalism. For a given component c, let T(c) be the set of all tasks that can be generated/executed in that component. Also, following the notation from [Teodorescu20b], we denote by t1 → t2 the fact that task t2 depends on task t1 being executed (dependency relation), and by t1 ~ t2 the fact that tasks t1 and t2 cannot be executed in parallel (restriction relation).
For representation simplicity, we also assume that whenever there is a dependency relation t1 → t2, there is also a restriction relation t1 ~ t2. After all, if one task depends on another task, the two tasks cannot run in parallel.
With these two relations, we can define the set of constraints for a component:
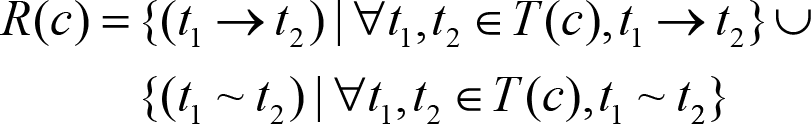
In addition, we also denote by spanw(t) the action of spawning a task t, and by S(c) the set of all the points in the component c where we spawn a task.
With these defined, then the three sets T(c), R(c), and S(c) completely define the task system for the component c.
Now, if we want to compose two components and into a bigger system , then the following would apply:
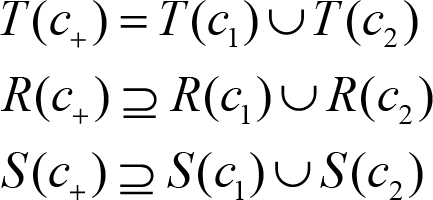
In plain English, the super-component contains all the tasks, relations and spawns of the two subcomponents, plus some more relations or spawn that might appear from the integration. The set of tasks is always the union of the two sets corresponding to the two sub-components; a task can be created either by one sub-component or by the other. But, when composing the two sub-components we may need to add relations between tasks coming from different sub-components. Similarly, we need to allow the code from one component to spawn a task from a different component.
There is an important assumption we are making: the set R(c) for a component is maximal. That is, if two tasks cannot be run in parallel, there must be a restriction connecting these two tasks (either direct or by transitivity). We do not consider subsets of R(c) which are not maximal, and two tasks are not executed in parallel for other, accidental, factors (i.e., some functions are never called into a particular order).
Lemma 1 (inner safety). When composing two or more task-safe components into a larger one, the internal safety of each component is not affected. i.e., one does need to add extra protection within any of these components to make the composed system safe.
Let’s assume that there are two tasks t1, t2 within one component c1, so that, when composing c1 with c2 into a super-component c+ we get a safety issue. To get a safety issue in c+ we need to be missing a dependency or restriction relation between the two tasks; formally (c1 ~ c2) ∉ R (c+). But because t1, t2 ∈ T (c1), the missing dependency or restriction relation must also be part of R (c1).
However, based on the above assumption, the set R (c1) is maximal. Together with the fact c1 that is tasksafe, this means that we cannot be missing any relation from R (c 1).
We reached a contradiction. Therefore, we cannot have two tasks belonging to one component that, when joined with other components will generate a safety issue. This means that adding an extra component to an existing component we do not compromise the safety of the first component.
Q.E.D.
Lemma 2 (overall safety). Composing two components that are task-safe, will make the resulting supercomponent also task-safe, assuming that the tasks have only local effects.
Before proving this lemma, let us discuss what do we mean by “tasks have only local effects”. The tasks in a component should affect only the resources owned by that component and should not have global effects. Of course that if two components have tasks that affect the global resources, then running two of such tasks in parallel, one from each component, might create a safety issue.
Let us prove this by contradiction. In order for the super-component to be unsafe, then there must be two tasks t1 and t2 that cannot be safely run in parallel, yet the composed system allows it. One alternative would be for the tasks to belong to the same component; but this cannot be true because of the previous lemma. Therefore, the only other alternative is for one task to be from a component and the other from the other component. But the tasks have only local effects. Thus, a task from one component cannot affect in any way the other component, so it cannot be unsafe to run it in parallel with another task from another component. This cannot be the case.
If neither of the two alternatives are plausible, it means that we cannot find two tasks that can run in parallel in the composed system, so the composed system is task-safe.
Q.E.D.
The reader should note that there are cases in which tasks have global effects. This doesn’t necessarily mean that the safety of the super-system is compromised; it means that when composing the two components we need to add constraints (dependencies or restrictions) between tasks belonging to different components. This is precisely the reason why we said that the set of relations for the super-component can contain elements that are not in the any of the sets of relations for the sub-components.
Lemma 3 (inner performance). The task execution throughput of a component does not decrease when it’s composed with other components, assuming there are no extra constraints added for the tasks belonging to that component, and that there are enough hardware resources.
Let qp(c) the maximum task execution throughput for component c, on a system with p cores: how many tasks are executed in a unit of time. This throughput is directly affected by the duration of the tasks and by the available parallelism. We assume infinite parallelism, and also, for simplicity let’s not bother with the duration of tasks and assume they are all equal – we are concerned with the general dynamics, rather than specific timings that the tasks might have.
If there would be no restrictions, set (R(c) = 0), then all the tasks can be executed in parallel, so q∞ = |T(c)|. The only way to reduce this is to add constraints on the tasks. So, the throughput is a function of the restrictions set: q∞ (c) = q∞ (N(c),R(c)).
Adding other components without adding extra restrictions will keep R(c) unchanged. Thus, all parameters being equal, the throughput remains the same. Q.E.D.
Please note that, in practice, the actual throughput is smaller than the maximal throughput. We never have all the tasks ready to start, and thus we only achieve a faction of this maximal throughput. The more tasks we spawn, the closer we get to the maximal throughput. Therefore, it may happen that, whenever other components are adding more spawns to the initial component, its throughput might actually grow.
On the other side, composing components with non-local tasks might require adding more constraints between tasks of different components. The more constraints, the less our throughput will be. A well-designed component, with very few tasks that have global effects will tend not to suffer from this problem.
Lemma 4 (overall performance). The total throughput of a system comprised of two components that have tasks with local effects will be the sum of the throughputs of the two components, assuming enough hardware resources.
The components have local tasks, so there will be no extra restrictions added to the overall system. Thus, taken independently the two components will not degrade their throughput. Now, considering that we have enough hardware resources, the tasks from two components can run completely in parallel. Therefore, the total throughput will be the sum of the individual throughputs. Q.E.D.
In practice, when the amount of parallelism is limited, the throughput will also be limited by the hardware constraints.
Again, the same discussions about tasks with global effects and about real-world throughput and maximal throughput apply here.
Also, as argued in [Teodorescu20a], one needs to be fully aware that in a real-world system there is always some indirect contention between the tasks, which may affect performance.
Theorem (composability of tasks systems). Components that have tasks with local effects can be composed in larger systems without any loss of safety or performance.
This follows directly from the above lemmas. Q.E.D.
Tasks systems will not have the same problems that the classical threads and locks approach would have.
Decomposing tasks into sub-tasks
So far, we’ve shown that tasks systems compose really well. If one has two components that are using tasks, they can easily be composed into a larger system while maintaining safety and performance. This is essential for a bottom-up approach. The questions that we are trying to answer in this section is whether is as easy to decompose task systems into smaller sub-systems; that is, how easy would it be to have a topdown approach to concurrency with tasks?
If we assume that the system is composed of generic tasks, then we can always have a partition of the tasks and relations, and have the decomposition around that partition. But if we have certain concurrent abstractions (e.g., a pipeline) that generate tasks then it might be harder to partition the tasks.
Also, we might need to take a large task and divide it into smaller tasks, so that they can be potentially run in parallel (under certain constraints). This may be relatively easy if the tasks are hand-made, but it may be more complicated if the tasks are generated by a concurrent abstraction (e.g., a pipeline).
Let us take a motivating example and try to fix all these cases. Let’s assume that we have a high-level pipeline processing in our component, one stage of that pipeline can be subdivided into smaller tasks. This actually comes from a real-world problem that I tried to solve recently.
Figure 1 shows a diagram of the problem. We have a pipeline with 4 stages, and the third stage contains more processing than the others, and can be potentially decomposed into smaller tasks. The amount of parallelism generated by the pipeline is relatively small, especially because the third stage needs to be executed in order. Thus, we would take great performance advantage from breaking a task from the third stage into multiple smaller tasks.
| Figure 1 |
The problem
The way that the pipeline abstraction is constructed, at each stage the body of the task is executed, and when that execution is finished, the pipeline checks to spawn the next tasks (next stage and the same stage of the next line). Given a task functor, the pipeline wraps it into another function that executes this task termination logic.
This composability of custom stage logic with pipeline logic is done inside a single task, in the single stack of execution and on a single thread. Thus, one cannot simply inject multithreaded execution on that thread / stack context.
A first attempt
One way of getting around this is by using the fork-join pattern [McCool12] [Robison14] [Teodorescu20c]. In Concore [concore], one can implement it similar to the code shown in Listing 4. One can spawn a lot of sub-tasks attached to a task_group and then wait for that task_group object, waiting on all these tasks to be complete.
void third_stage(LineData& line) {
auto grp = concore::task_group::create();
// Create some sub-tasks
concore::spawn([&line]{ f1(line); }, grp);
concore::spawn([&line]{ f2(line); }, grp);
concore::spawn([&line]{ f3(line); }, grp);
// Ensure that all the tasks are executed
// before continuing
concore::wait(grp);
}
|
| Listing 4 |
From a high-level perspective, this gives us what we need: we can create sub-tasks inside a pipeline stage, and parallelise the stage more. The wait operation is going to be a busy wait, so, in terms of throughput we are ok, assuming that we have enough tasks to be executed.
But this solution can introduce high latencies, and may not work well when we don’t have too many tasks to be executed, like in our case. The problem is that the wait() call will try to execute any task that it can, hoping that the tasks from the group will finish early. It provides no guarantee that the tasks spawn in the same context will be executed first. Thus, we can arrive in a situation that we execute all the other tasks before we can actually execute the tasks that we need. If we don’t have enough tasks in the system, we may actually drain the tasks from the system, leading to reduced throughput.
For example, in our pipeline problem, such a wait() call may execute all the stages/lines that can be executed before the stage is completed. This will essentially reduce the entire parallelism to the completion of one task.
This solution is relatively simple and can work in certain cases, but it will not solve all the needs for decomposition.
A better solution
Let us derive a general solution that will not have this performance problem.
First, going back to the theory from [Teodorescu20b], we argued that a task system implementation needs to have some special logic in two places to function properly. The first one is at the task creation, and the second one is at the completion of the task. We are going to focus on the latter one.
If one defines a task as a wrapper over std::function<void()>, then the logic that happens on task completion must be manually encoded in the body of the functor. For many structures that are built on top of these tasks (pipeline, task serializers, task graphs, etc.) each time the user pushes a task into it, another wrapper functor is created that contains the original task logic, plus the continuation logic.
If fn is the function that needs to be executed at the stage n, then the pipeline actually constructs a task that executes the wrapper function wn (fn, cn), ensuring that after executing the user task the pipeline advances. Ignoring the error handling code, we can say that wn is just executing cn after fn.
Traditionally, cn is executed within the same stack, and on the same thread as fn, but if we look more carefully, this doesn’t need to be true. We can call cn from a different thread, a different context; as long as we will call it, the pipeline can advance. This starts to resemble the continuation pattern [Teodorescu20c].
Let us formalise this, prove that it can actually solve our problem and prove that it can be applied generically to similar problems.
Instead of a task t (f) that takes a user-supplied functor to be executed, we will introduce a new type of task of the form w (f, c). The execution of an old-style task was defined as execute (t (f )) = f ( ). For the new task, we define execution as execture (w (f, c)) = f( ); c( ) – that is, first execute the functor f then the functor c. All the other elements of the task system (spawning, constraints, etc.) remain the same.
Lemma 5 (equivalence). A task system using new tasks of the form w (f, c) can be used to model all the problems that can be solved with old task types t (w), with the same performance.
The proof follows directly from the realisation that we can always construct the new tasks with an empty continuation functor, such as:
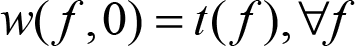
Q.E.D.
After this equivalence lemma, we will use the new set of tasks in our higher-level concurrency abstractions. We will consider that all the user-supplied functors will be placed in the part untouched, while the code needed to make the abstraction work we will put in the part, without mixing the user-supplied functors with the functors needed for realising the constraints of the abstraction. A concurrency abstraction that has this division, and that does not impose any restrictions on which threads the continuations are called will be called from now on a continuation-based concurrency abstraction. One can make abstractions like pipeline, the task serializers, task graphs, and a continuation abstraction [Teodorescu20b] as continuation-based concurrency abstractions.
Any continuation-based concurrency abstraction runs independently of the user-supplied functors (if they do not try to interact with the abstraction itself). Thus, regardless of the user-supplied functions, a pipeline will have the same execution pattern. Focusing on the continuations will allow us to assess the properties of the abstraction itself; in particular we are interested is seeing if various transformations will keep the abstraction running.
A key point in how we defined these continuation-based concurrency abstractions is that if the continuations are executed in the same order (possible from different threads), all the properties of the abstractions will remain the same. Thus, if one moves the execution of a continuation from a thread to another thread, the abstraction will still function.
Lemma 6 (task decomposition). A continuation-based concurrency abstraction that executes a task w0 ( f0,c0) can be transformed so that it executes an arbitrary graph of tasks G = {w1, w2, …,wn}(that ends its execution with a task wn) instead of task w0, without changing the functioning of the continuation-based concurrency abstraction.
The key here is to exchange the execution of w0 with the execution of G, and ensure that c0 is called at the end of the execution of G. If we can do that, then, based on what we observed above, the continuation-based abstraction will function the same.
For this, we will define cn' = cn ;c0 (call cn then c0) and (replace the continuation in wn), and G' = {w0, w1, …,wn'} (replace the last task from G). We also define f0' = execute(G') and w0' = (f0',0).
Now, if we exchange w0 with w0', the continuation c0 is still called when everything else finishes to execute. This means that we can safely exchange w0 with w0' in our continuation-based abstraction, without affecting the functioning of the abstraction. Q.E.D.
Theorem (task decomposition generality). For any concurrency abstraction that can be turned into a continuation-based concurrency abstraction, one can decompose tasks into smaller tasks (possible running in parallel), without affecting the overall properties of the abstraction.
This follows directly from the above lemmas. Q.E.D.
Listing 5 shows how this technique can be applied in concore1, to avoid the blocking-wait from Listing 4.
void third_stage(LineData& line) {
auto* cur_task = concore::task::current_task();
auto cur_cont = cur_task->get_continuation();
// Create the final task, with the current
// continuation
concore::task t_final{f_final, {}, cur_cont)};
// Clear the continuation from the current tasks
cur_task->set_continuation({});
// Create some more tasks
concore::spawn([&line]{ f1(line); });
concore::spawn([&line]{ f2(line); });
concore::spawn([&line]{ f3(line); });
// we assume that after these tasks are executed,
// t_final will be called
}
|
| Listing 5 |
We have now a good way to take a top-down approach to our concurrency: use the most appropriate (continuation-based) concurrency abstraction, then, where more concurrency is needed, decompose a task into smaller tasks.
Conclusions
This article explores composition and decomposition of task-based systems. If classical threads and locks systems are hard to compose properly, with tasks this seems to be an easy task (pun intended).
With threads and locks, composition can easily lead to safety problems. To protect against these safety issues, one must always work at the interfaces between components and strengthen the protection. This is typically done by adding more locks, and this can downgrade the performance.
With task systems, we show that, for most cases, good composability is achieved without sacrificing safety and performance, and without any additional effort. The cases that need special attention are the cases in which tasks from one component have a global effect, and they are not safe to run in parallel with tasks from another component.
A good design would limit the number of tasks with global effects, so the amount of extra work, and the performance degradation would be limited.
Then we turn our attention to the decomposition of tasks. We show that, higher level concurrency abstractions based on continuations can easily be used to with task decomposition. We can break down a larger task into smaller ones, without affecting the functionality of the abstraction from which the task belonged to.
This is crucial as it would allow us to approach concurrency in a top-down manner. One first finds the right abstraction at the higher level, then decomposes different parts of that high-level abstraction into smaller one. This process can be repeated until we reached the desired level of concurrency.
Concurrency design is no longer dependent on the details of implementation, it doesn’t need to be a bottom-up approach. One can design the concurrency of the application upfront, in a top-down, like any other software design activity.
Concurrency design doesn’t need to be a hard thing.
References
[concore] Lucian Radu Teodorescu, Concore library, https://github.com/lucteo/concore
[Lee06] Edward A. Lee, The Problem with Threads, Technical Report, 2006, https://www2.eecs.berkeley.edu/Pubs/TechRpts/2006/EECS-2006-1.pdf
[McCool12] Michael McCool, Arch D. Robison, James Reinders, Structured Parallel Programming: Patterns for Efficient Computation, Morgan Kaufmann, 2012
[Robison14] Arch Robison, A Primer on Scheduling Fork-Join Parallelism with Work Stealing, Technical Report N3872, http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2014/n3872.pdf
[Teodorescu20a] Lucian Radu Teodorescu, Refocusing Amdahl’s Law, Overload 157, June 2020, available online at: https://accu.org/journals/overload/28/157/teodorescu_2795/
[Teodorescu20b] Lucian Radu Teodorescu, The Global Lockdown of Locks, Overload 158, August 2020, available online at: https://accu.org/journals/overload/28/158/teodorescu/
[Teodorescu20c] Lucian Radu Teodorescu, Concurrency Design Patterns, Overload 159, October 2020, available online at: https://accu.org/journals/overload/28/159/teodorescu/
Footnote
- Continuation-based concurrency abstractions are just in infancy in concore. The syntax might change in the near future.
has a PhD in programming languages and is a Software Architect at Garmin. He likes challenges; and understanding the essence of things (if there is one) constitutes the biggest challenge of all.











