Locks can be replaced with tasks. Lucian Radu Teodorescu shows us how.
In the previous article [Teodorescu20], we showed how one can achieve great speedups using tasks as the foundation for concurrent programming instead of locks. The one thing that is not clear is whether one can use tasks for all the concurrent algorithms1. Tasks may be applicable to certain types of problem, but not to all problems. This article tries to complete the picture by showing that all algorithms can use tasks and there is no need for locks.
We prove that one can find a general algorithm for implementing all concurrent algorithms just by using a task system, without the need for locks or other synchronisation primitives in user code.
Hopefully, by the end of the article, the reader will be convinced that locks should not be used in day-to-day problems but instead should be confined to use by experts when building concurrent systems.
Task systems and task graphs
Let us recap from the previous article a few notions about what it means to have a task system:
- The work of the algorithm is represented by tasks; a task is an independent unit of work.
- We add constraints between tasks, modelling dependencies and possible race conditions.
- There is an execution engine that can take tasks and execute them dynamically on the various cores available on the running machine. The execution engine is typically greedy, meaning that it executes tasks as soon as it has hardware resources.
One key point here is that the tasks are independent. Two active tasks should never block each other. (We’ll discuss the meaning of active tasks below.) As shown below, all the constraints between tasks can be implemented on top of such a task system. The task system framework may provide facilities to ease this work, but this is not essential.
As examples of task systems, we have Concore [concore] or the more popular Intel Threading Building Blocks [tbb]. The few examples in this article will be written using Concore, as it is the library I’m developing while trying to make sense of the concurrency world.
It is obvious that all algorithms can be expressed in terms of non-blocking tasks, possibly with some threads that don’t have tasks to be executed (or colloquially waiting for them to be unblocked). At the bare minimum, one can wrap any non-blocking instruction in a task (very inefficient, but possible); however, in general, a task will be a set of instructions that make sense to be considered as one unit, both from the semantic point of view and from the constraints point of view.
Tasks may have dependencies or restrictions between them. If two tasks A and B can be safely run in parallel, then there is no dependency or restriction between the two of them. If task A needs to finish before executing B we say that there is a dependency from A to B; we denote that by A→B. If the two tasks cannot be safely run in parallel, but the order in which we run them is irrelevant, then we say that there is a restriction between them; we denote that by A ~ B. A restriction between two tasks can always be turned into dependency by arbitrarily choosing which task needs to be executed first. For example, if two tasks write the same data, we typically want to create a restriction between them; not doing so will probably result in race condition bugs.
For efficiency reasons, we consider the tasks to be as small as possible, with respect to the constraints between them. That is, if only a small part of task A has constraints with other tasks, then we would break up task A into smaller parts, to minimize the scope of the constraint.
The dependency is transitive, but the restriction relation is not. If we have three tasks A, B and C, with A→B and B→C, then A→C; for a given task we can always find the transitive closure for the dependency relation. On the other hand, if A ~ B and B ~ C, it doesn’t imply that A ~ C: tasks A and C could be run in parallel. Also, it’s important to note that the restriction relation is commutative (while the dependency is not).
Let us denote by succ(A) the set of tasks given by the transitive closure of the dependency relation. Also, let us denote by pred(A) the set of tasks X for which A ∈ succ(X) (i.e., all the predecessors of task A).
With these notions set, a task A can be executed in isolation if pred(A) = Ø. Also, a set of tasks S can be executed in parallel, if for each task X in that set pred(X) = Ø, and ∄X,Y ∈ S such as X ~ Y; we call S to be a parallel set of tasks. These are the conditions that we need for executing the tasks.
The reader should pause a bit and digest the information above. Basically, we have expressed in algebraic form the safety conditions for executing tasks. We defined the constraints in such a way to eliminate possible data race bugs.
A more intuitive way is to represent all these with graphs of tasks. Figure 1 shows an example; most of the links between tasks are dependencies, but we also have restrictions T9 ~ T13 and T14 ~ T15.
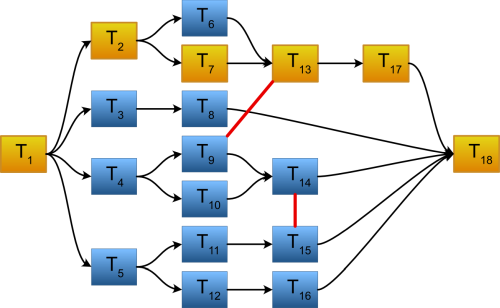 |
| Figure 1 |
Representing the concurrent algorithm as a graph is highly encouraged. Software developers tend to reason better on the algorithm if it is expressed visually as a graph than if it’s expressed as a set of rules. Knowledge of graphs is deeply rooted in the software engineering mindset. This can help both at algorithm design and at understanding the performance consequences of the algorithm.
For example, one can easily check what are the tasks that can be run in parallel. In our case, task T6, T7, T8, T9, T10, T 11 and T12 can safely be run in parallel, and so are the set of tasks T2, T8, T14, T11 and T16.
A general method for executing algorithms concurrently
We need to distinguish some time-points relevant to the algorithm execution:
- The point at which a task can be created (we have all the data needed; we know about its constraints with existing tasks) – this is typically different from the time the task can start executing
- The point at which the task can start executing
- The point at which the task finishes executing
We will construct a general method that will have logic at the creation of the task and at the point at which the task finishes executing to determine the point of execution start for all the tasks. We are building a scheduling algorithm.
To do so, we need to divide the tasks into three groups: finished, active and pending tasks. Finished tasks are, as the name implies, tasks that were completely executed. Active tasks are either tasks that are in progress or tasks that can be started at any given point. Because we have a limited number of cores, we cannot guarantee that all the active tasks start immediately; for example, on an 8-core machine, we will start executing 8 tasks, even if there are 1000 active tasks. Finally, pending tasks are tasks that cannot be executed right away, as some constraints are not satisfied; i.e., not all the predecessors are finished, or there is a restriction task with some task that is currently active.
The key point of this division is that all the active tasks might be executed in parallel given enough hardware resources. That is, all the predecessor tasks for them are completed, and there is no restriction relation between any two active tasks. That is, the set of active tasks at any given time is a parallel set of tasks as described above.
A task can be in any of the three groups at different times. The valid transitions are pending to active, and active to finished. No other transition is allowed.
It is obvious that we transition an active task to finished after the task execution is complete. Maybe less obvious, but still straightforward is the transition between pending and active; we make this transition as soon as possible, as soon as the constraints of the tasks disappear. The only caveat here is that we need to have a holistic approach. It may be the case that two tasks A and B can be both independently transitioned from pending to active, but not together at the same time, as A ~ B. In this case, we can choose one task and add it to the active group, while keeping the other to the pending group. In other words, transitioning from pending to active needs to be done one task at a time.
With this, we can finally describe the general method. It amounts to 4 steps:
- Ensure we have at least one active task at the start of the algorithm
- Keep track of the state of all the tasks and constraints between them
- Add some special logic when a task needs to be created and when a task finishes executing; this is presented in pseudo-code in Listing 1.
- Whenever a task becomes active, add it to the task system so that it can execute it.
void executeTask(task& t) {
assert(isActive(t));
// the body of the task 't'
{
…
// at any point that a task 'new_task' can be
// created
if (canTaskBeActive(new_task))
spawnActive(new_task);
else
spawnPending(new_task);
…
}
moveTaskToFinished(t);
for ( auto t2: pendingTasks() )
if (canTaskBeActive(t2))
moveTaskToActive(t2);
}
|
| Listing 1 |
At the end of the executeTask() function, we decide which of the pending tasks can be moved to active. For simplicity, we consider here that we will iterate over all the pending tasks. But that is overkill; in practice, we should look only at the tasks that are either successor of the current task or that have a restriction relation with it.
The key to this algorithm is the decision of whether the task can be active or not. It needs to be done whenever a task can be created, and at the end of running the tasks, when pending tasks can be made active. This is a greedy algorithm as it tries to move to active as many tasks as possible, without considering that there may be combinations in which holding up tasks may lead to better parallelism. In practice, this tends to work really well due to the scheduling non-determinism.
A possible implementation of the test to check if a task can be active is given in Listing 2.
bool canTaskBeActive(task& t) {
for ( auto t2: directPredecessorOf(t) )
if (!isFinished(t2))
return false;
for ( auto t2: restrictionsOf(t) )
if (isActive(t2))
return false;
return true;
}
|
| Listing 2 |
Let us now prove that this scheduling algorithm can safely and efficiently be used to implement any concurrent algorithm that is properly divided into tasks.
Lemma 1 (termination). If the concurrent algorithm needs a finite set of finite tasks that do not have dependency cycles, then the scheduling algorithm will eventually execute all the tasks, leading to the completion of the algorithm.
We start with at least one active task, and by the problem description, we are always going to finish executing the current set of active tasks.
If there are pending tasks, by executing all the currently active tasks at least one pending task will be transitioned to active (as seen above this transition happens greedily, as soon as possible). By the fact that the tasks don’t have dependency cycles, and as the number of tasks is finite, there must be at least one task A in the pending group that doesn’t have dependent tasks in the pending group. By construction, we put task A in the pending group only if there is an active task B such as B→A or B ~ A. But B is guaranteed to finish at some point; at that point, task A can become active. And, by the construction of our scheduling algorithm, we always check what tasks can be transitioned to active whenever a task completes. Therefore, A will be transitioned to active whenever B completes. That shows that we are always making progress.
As we start with a non-empty set of active tasks and we are always making progress, we eventually will execute all the tasks in the algorithm (remember, the algorithm has a finite set of tasks).
Q.E.D.
Lemma 2 (soundness). If the dependencies and restrictions between the tasks are set correctly (i.e., if two tasks can cause a race condition bug, then there must be restriction between them or a dependency chain), the scheduling algorithm will never schedule two tasks at the same time that can cause race condition bugs.
By the construction of the algorithm, we cannot execute in parallel tasks that are not present in the active group at the same time.
We add to the active group one task at a time. Let’s say that A and B are active tasks, with A added before B. Both tasks could not have non-finished predecessors, as otherwise they would not have been added to the active group; so there can’t be a dependency between them. Also, it can’t be that A ~ B as B would not have been added to the active group. Thus, there can be no incompatibility between the tasks in the active group. If there can’t be any incompatibility between two active tasks, and we never have in execution tasks that are not in the active group at that time, we can’t have two incompatible tasks in execution at the same time.
Q.E.D.
Lemma 3 (efficiency). On a machine with infinite task parallelism, at any given point in time (except points in which we are running the scheduling logic) one cannot schedule for execution another task while maintaining the soundness of the algorithm as expressed just by the constraints between the tasks.
Please note that this aims for the efficiency of a greedy algorithm. In other words, this scheduling algorithm ensures a local maximal capacity, and not necessarily a global optimum. Again, due to timing non-determinism, a greedy scheduling works well in practice.
A key point of this lemma is to ignore the time spent by the scheduling algorithm. Of course, there is a small window of time, while we are deciding which task to make active, in which that task can be active and it isn’t yet. We are just focusing on the times in which all the queued tasks are still executing.
Also, it’s important to note that as we are looking at the incompatibility between tasks as expressed just by the constraints between the tasks, the constraints between tasks apply for the whole duration of the tasks. In other words, we cannot say that a constraint for a task vanishes after a task executes half-way through. The tasks are atomic with respect to constraints.
Let us assume that S is the current set of active tasks and that B is a task still in pending state, but that can be run without being unsound. But, if B can be safely run, it means that it can be an active task. So, if B could be an active task and it isn’t, it means that there was a point in time at which B could have been categorised as active (but the scheduling algorithm didn’t). In other words, there must be a time when the active constraints for task B change. As the tasks are atomic, these constraints can only happen when B is created, or whenever a task A for which A→B or A ~ B is completed. But the algorithm covers both cases: both when B is created and whenever another task finishes, we re-evaluate whether B can be moved to the active group. So, there cannot be another time in which B could be scheduled, and B is added to the active group as soon as it possibly can. This means that our scheduling algorithm always guarantees that the set S of active tasks is always at its maximal capacity (assuming a greedy strategy of creating this set).
Q.E.D.
Theorem. There is a scheduling algorithm that can be used to schedule the execution of any concurrent algorithm properly expressed with tasks and constraints between tasks; the scheduling algorithm has the maximum efficiency it can have with greedy scheduling.
The proof follows immediately from Lemma 1, Lemma 2 and Lemma 3.
Q.E.D.
In this section we constructed a general scheduling algorithm that can be used to solve any type of concurrent algorithms, we proved its viability and that its theoretical efficiency is maximal. However, in practice, we don’t necessarily need a general/global algorithm for scheduling. We can instead have smaller scheduling algorithms that can be used to solve various types of common problems, and then we can easily compose them to get an overall scheduling algorithm. Let’s look at a few such particular scheduling algorithms
Replacing locks
Most probably the reader is familiar with solving concurrency problems by utilizing locks. Thus, probably it will be easier to just have a direct translation of problems that can be solved with locks into problems that can be solved with tasks. We will present three specialised schedulers to cover the same effect as one would traditionally cover with mutexes, semaphores and read-write mutexes.
The serializer
Let us attempt to model the behaviour of a mutex with tasks. A mutex protects one of the multiple regions of code against access from multiple threads. For simplicity, let us assume that the entire region covered by a lock is atomic – there are no other locks in it, and the parallelisation constraints with other regions do not change midway. This assumption is an invitation to make that zone of code a task. We would actually have tasks for all the invocations of the zones protected by the mutex.
If the mutex M protects zones/tasks A1, A2, …, An then the run-time effect of the mutex would be similar to imposing restrictions between any of the tasks: Ai ~ Aj,∀i,j.
Therefore, we can introduce the so-called serializer, as a local scheduler that can accept tasks and ensure that there are restriction relations between all the tasks enqueued in it. As any two tasks enqueued into it will have a restriction between them, a serializer will only schedule one task at a time for execution – therefore the name: serializer.
Figure 2 shows the restriction relationships between 4 tasks that can be enqueued into a serializer, while Figure 3 shows a possible execution order.
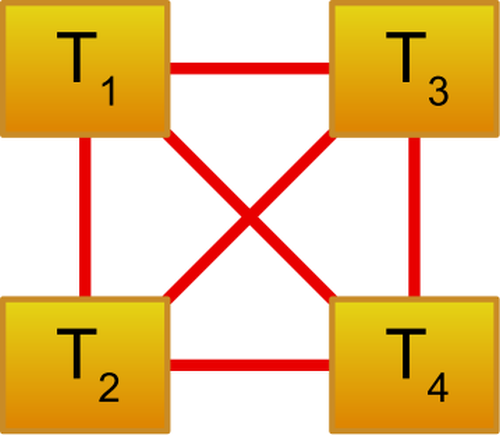 |
| Figure 2 |
 |
| Figure 3 |
The implementation of a serializer can be easily made in the following way:
- the abstraction should have a method of enqueueing a task into the serializer
- keep a list of pending tasks that are enqueued in the serializer but are not yet executed; also keep track of whether we are executing any task or not (i.e., by using an atomic variable)
- whenever a new task is enqueued, if there is no other task in execution, start executing the new task
- whenever a new task is enqueued, if there is another task in execution, add it to the pending list
- whenever a task finishes executing, check if there are other tasks in the pending list; if the answer is yes, start executing the first task in the pending list
The serializer can be implemented relatively easily in about 100 lines of C++ code. If the reader is curious, I would invite the reader to check the implementation inside the Concore library.
Listing 3 shows an example of using a serializer in Concore. We assume that the application needs to have backups of the main data at a certain point, two backups cannot run in parallel, and the way the application is constructed, one can trigger the backups from multiple threads/tasks, possible in parallel.
concore::serializer my_ser;
backup_engine my_backup_engine;
void trigger_backup(app_data data) {
my_ser([=]{ my_backup_engine.save(data); });
}
|
| Listing 3 |
Regardless of how many threads will call trigger_backup(), the backup engine’s save() method will not be called in parallel from multiple threads. Simple, right?
n_serializer
A semaphore is in one way a generalisation of a mutex. Instead of allowing only one region of code to be executed in parallel, it allows N such regions, based on how the semaphore is configured. Semaphores can be used in different ways too (for example, as notification primitives), but let us focus on protecting regions of code. From this perspective, if we translate this in terms of tasks, we can say that the effect would be to allow N tasks to run in parallel.
To provide such an abstraction, Concore implements the n_serializer class. It is similar to serializer but it allows a configurable number of tasks to be run in parallel. The implementation follows the same pattern as for the serializer, so we won’t describe it here.
Let us also give an example of how to use an n_serializer with Concore. To continue the previous example, let’s assume that saving a backup can be an expensive operation, so that it can queue up in certain cases, producing delays in saving the backups; for performance reasons, we want to create multiple backup engines that save the backups at different locations in parallel. Listing 4 shows how this can be implemented with Concore.
concore::n_serializer my_ser{10};
concore::concurrent_queue<backup_engine>
my_backup_engines; // at least 10
void trigger_backup(app_data data) {
my_ser([=]{
// acquire a free backup engine
backup_engine engine;
bool res = my_backup_engines.try_pop(engine);
assert(res);
// do the backup
engine.save(data);
// release the backup engine to the system
my_backup_engines.push(std::move(engine));
});
}
|
| Listing 4 |
The example shows a bit more than just the serializer; it also showcases the use of a concurrent queue to operate on multiple data objects from different tasks in parallel. Again, simple enough.
rw_serializer
Another generalisation of a mutex is a read-write mutex. This type of mutex allows multiple “read” operations to execute in parallel but does not allow any “write” operations to be executed in parallel with any other operations.
Just like in the previous two cases, we can express read-write mutexes with tasks. We create two types of tasks: read tasks and write tasks. The read tasks can be executed in parallel, but write tasks cannot be executed in parallel with read tasks or other write tasks. The runtime constraints between them are relatively straight-forward: just create restriction constraints between write tasks and everything else. Figure 4 shows an example of how we can encode 5 read tasks and 2 write tasks.
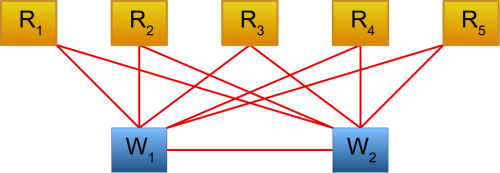 |
| Figure 4 |
The implementation of such an abstraction is slightly more involved than the implementation of a serializer. For this, we need to have two queues of tasks: one for read tasks and one for write tasks. Then we need to decide which tasks take priority: write tasks or read tasks. An implementation that favours write tasks will not execute any read tasks while there are write tasks in the pending queue. Conversely, an implementation that favours read tasks will not execute any write tasks while there are read tasks; continuously adding read tasks may make the write tasks starve. After deciding which type of task has priority, the implementation follows the same pattern, with the caveat that it’s more difficult to ensure atomicity for various operation in a multi-threaded environment. Slightly more complex, but not necessarily hard.
Concore implements an abstraction for this type of problems called rw_serializer. Its implementation favours write tasks over read tasks.
To exemplify this type of abstraction, let’s consider the case in which we want to allow easy querying of information from the backup engine, but doing a backup cannot run in parallel with any querying operation. As opposed to our previous example for n_serializer, we consider that the save operations are relatively easy to perform, and they occur less frequently. Listing 5 shows how this can be implemented with Concore.
concore::rw_serializer my_ser;
backup_engine my_backup_engine;
void get_latest_backup_info(backup_info& dest,
concore::task& next) {
my_ser.reader()([&dest, &next] {
// query backup data
dest = std::move(my_backup_engine.get_info());
// query is done; continue with a new task after
// the data is ready
concore::global_executor(std::move(next));
});
}
|
| Listing 5 |
The above example also showcases how task continuations can be implemented by hand, in the absence of more elaborate scheduler. Again, simple.
Replacing locks, discussion
In this section, we showed that one can build local schedulers to replace locks with tasks. They provide convenient ways to attack the problem and, in terms of implementation, they are more efficient than a general scheduling algorithm. If one’s application can be relatively easily translated into tasks, using these serializers should be straight-forward.
However, there are a few complications. I cannot properly end this article in a very positive manner without touching on the main problems that one would face whenever one would try to put this into practice. So, here they are:
- How can we add a section of code/task in two serializers at once (i.e., like taking two locks for a region)?
- How can we break down the code to protect a zone of code in the middle of a task?
The first question discusses the composability of two task schedulers. Without entering in too many details we will just state that tasks are more composable than locks. Locks are known for not being composable [Lee06]. On the other hand, given two task schedulers, we can compose them, even without knowing their inner structure. There are multiple ways of doing this, but probably the most prominent method is the fork-join model [McCool12, Robison14]; this is the default programming model for both Cilk [cilk] and its successor CilkPlus [cilkplus]. The main idea is that, while executing a task, one can fork (spawn) a new task, and later on wait for that task to complete.
In our case, one would enqueue one task in a serializer that would enqueue-and-wait another task in the second serializer, and this second task will actually do the work. Listing 6 provides a quick example of composability. It’s not complicated to do such a thing. The logic is a bit wired, but that’s inherent to the problem that we are trying to solve; one if far better to avoid mixing multiple scheduling systems for the same task (in terms of locks; avoid using multiple locks to protect certain regions).
concore::serializer my_ser1, my_ser2;
void double_serialize(std::function<void()> work) {
my_ser1([work = std::move(work)]{
concore::spawn_and_wait([work =
std::move(work)]{
my_ser2(work);
});
});
}
|
| Listing 6 |
The second problem may not be apparent when looking from a theoretical perspective, but it’s immediately visible when trying to change an existing system that currently uses locks to use tasks instead. Let’s assume that one has an application that can be broken down in tasks relatively easily. But, at some point, deep down in the execution of a task one would need a lock. Ideally one would break the task in 3 parts: everything that goes before the lock, the protected zone, and everything that goes after. Still, easier said than done; this can be hard if one is 20 layers of function-calls – it’s not easy to break all these 20 layers of functions into 3 tasks and keep the data dependencies correct.
If breaking the task into multiple parts is not easily doable, then one can also use the fork-join model to easily get out of the mess. A sample code is shown in Listing 7.
concore::serializer my_ser;
void deep_fun() {
some_work();
concore::spawn_and_wait([=]{
my_ser([=]{ my_protected_work(); });
});
some_other_work();
}
void fun_with_depth(int level) {
do_pre_work(level);
if (level > 0) fun_with_depth(level-1);
else deep_fun();
do_post_work(level);
}
fun_with_depth(20);
|
| Listing 7 |
This technique is very useful not just for transforming locks into tasks. It can be used also to break applications into tasks that are used in other ways – for example, to model some asynchronous flows.
With that, we covered the two most prominent problems that people might have. Oh, wait… we still need to have *that* discussion on performance.
Performance
The sceptic reader might argue that using serializers is no better than using a mutex. After all, all the tasks are executed one after the other, without exercising parallelism. And yes, the last statement is true.
The key point of the serializers is that they do not block any threads. Threads can still be free to execute other tasks while certain tasks need serial execution.
Let’s try an analogy. Mutexes are like intersections (Kevlin Henney has nicely explained this in [Henney18]). While a car goes through an intersection, all other cars from the adjacent roads are blocked. If a city has a lot of crowded intersections, then traffic congestions can easily spread across large parts of the city – severe losses in the performance of the traffic system. Serializers are like (isolated) drive-throughs – the cars are waiting in line for the cars in front of them to be served (n_serializers can be associated with drive-ins). But the key point here is that these drive-throughs have sufficiently lengthy lanes – the cars waiting at the drive-through are not blocking the nearby intersections. In this case, the number of cars that can circulate compensates for a few cars that are waiting in the queue.
Hope that clears the performance worries for most of the readers. However, some astute readers might still wonder about the performance of the fork-join model, since we invoked it twice as a solution to common problems. Of course, they would argue, the performance of the application is affected when we are waiting for tasks to complete. But this is not the case. Most libraries these days (and Concore is one of them) can implement busy-waiting – that is, execute other tasks while waiting on a task to complete. With such a strategy, we are not blocking the worker threads, so we are still fully utilising the CPU to do real work.
Conclusions
The previous article [Teodorescu20] showed that if one can make a concurrent algorithm with tasks, it can obtain good parallel speedups (under certain conditions), especially when compared with using mutexes. This article proves that any concurrent algorithm can be implemented safely and efficiently with tasks and completely avoid mutexes. Thus, there is no reason to use mutexes anymore in high-level code.
Besides the proof, the article showed that one can use simpler structures (serializers) to move away from lock-based synchronisation primitives towards tasks, and that it is not a complicated endeavour. Another argument that we need to stop using mutexes.
So, please, please, please, unless you are building low-level concurrency primitives, avoid using mutexes, just like you avoid gotos (which I hope you are already avoiding).
The article also started to explore a few patterns that can be used for concurrent programming. The point was not to showcase the most important patterns, but to somehow exemplify the concepts discussed here and show that it isn’t hard to put them in practice. However, these hints oblige me to provide a follow-up article that explores patterns for designing concurrent applications; after all, software engineering is about design issues far more than it is about coding.
References
[cilk] MIT, The Cilk Project, http://supertech.csail.mit.edu/cilk/
[cilkplus] Intel, Cilk Plus, https://www.cilkplus.org
[concore] Lucian Radu Teodorescu, Concore library, https://github.com/lucteo/concore
[Henney18] Kevlin Henney, Concurrency Versus Locking, https://www.youtube.com/watch?v=yz1hypSTjvk
[Lee06] Edward A. Lee, The Problem with Threads, Technical Report UCB/EECS-2006-1, 2006, https://www2.eecs.berkeley.edu/Pubs/TechRpts/2006/EECS-2006-1.pdf
[McCool12] Michael McCool, Arch D. Robison, James Reinders, Structured Parallel Programming: Patterns for Efficient Computation, Morgan Kaufmann, 2012
[Robison14] Arch Robison, A Primer on Scheduling Fork-Join Parallelism with Work Stealing, Technical Report N3872, http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2014/n3872.pdf
[tbb] Intel, Threading Building Blocks library, https://github.com/oneapi-src/oneTBB
[Teodorescu20] Lucian Radu Teodorescu, ‘Refocusing Amdahl’s Law’, Overload 157, June 2020, https://accu.org/journals/overload/28/157/teodorescu_2795/
Footnotes
- As in the previous article, we use the term algorithm to denote a general problem that we need to solve; should not be mistaken for well-known algorithms in computer science.
has a PhD in programming languages and is a Software Architect at Garmin. As hobbies, he is working on his own programming language and he is improving his Chuck Norris debugging skills: staring at the code until all the bugs flee in horror.











