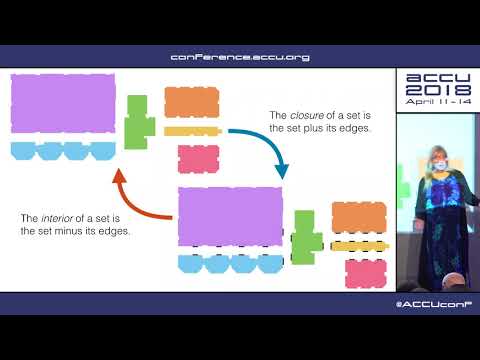
When we talk about programs, we often use metaphors of space: we speak of connection and separation, of paths and boundaries, of areas and lengths. We clearly have some intuition that sees a program as a shape.
In this talk, I will take this intuition seriously, applying topology, the fundamental mathematics of space. I will show how a program can be mathematically described as a shape ― a bitopological manifold ― arranging actions and capabilities in a frame of time, space, causality, and possibility.
No previous knowledge of topology will be assumed.
Advertisement
