Concurrency is a complicated topic. Lucian Radu Teodorescu provides a simple theory of concurrency which is easy to reason about and apply.
One of the big challenges with concurrency is the misalignment between theory and practice. This includes the goals of concurrency (e.g., improving the performance of the application) and the means we use to achieve that goal (e.g., blocking primitives that slow down the program). The theory of concurrency is simple and elegant. In practice, concurrency is often messy and strays from the good practices of enabling local reasoning and using structured programming.
We present a concurrency model that starts from the theory of concurrency, enables local reasoning, and adheres to the ideas of structured programming. We show that the model can be put into practice and that it yields good results.
Most of the ideas presented here are implemented in a C++ library called concore2full [concore2full]. The library is still a work in progress. The original goal for this model and for this library was its inclusion in the Hylo programming language [Hylo]. For Hylo, we want a concurrency model that allows local reasoning and adheres to the structured programming paradigm. We also wanted a model in which there is no function colouring [Nystrom15], in which concurrency doesn’t require a different programming paradigm.
This article is based on a talk I gave at the ACCU 2024 conference [Teodorescu24]. The conference was great! The programme selection was great; there was always something of interest to me. With many passionate C++ engineers and speakers, the exchange of information between participants was excellent; as they say, the best track was the hallway track. I highly encourage all C++ enthusiasts (and not just C++) to participate in future ACCU conferences.
What is concurrency?
Before we actually define concurrency, it’s important to draw a distinction between what the program expresses at design-time and its run-time behaviour. There might be subtle differences between the two. For example, even though the program expresses instruction A before instruction B, at run-time, the two instructions might be executed in reverse order (if there is no dependency between them) [Wikipedia-2]. In this respect, at program design-time we express a range of run-time possibilities, without prescribing a precise run-time behaviour.
Another example, more appropriate to our article: the code may specify that there needs to be two threads that execute some work, but we don’t know at run-time if the two work items are executed in parallel or whether the execution hardware somehow sequences them. It may happen that at run-time we have only one core available to execute the two work items, and thus we execute them serially. The original program expresses more possibilities than the actual execution.
More formally, we say that the execution of the program is a refinement of the program description written in the code. The execution is more determinate than the original program; it is more predictable and more controllable, and adds further decisions compared to the original program. See [Hoare14] for a more formal description of refinement, and how this can be applied to concurrency.
From a run-time perspective, we can define concurrent execution as the partial ordering of work execution (as opposed to non-concurrent execution, which is a total ordering of work execution). If we denote this ordering relation with ≤, then the following rules apply:
A ≤ A
A ≤ B, B ≤ C => A ≤ C
A ≤ B, B ≤ A => A = B
This means that, for two work items A ≠ B, there are only three ways in which execution can happen:
- A < B
- B < A
- neither A < B, nor B < A; we denote this by A ∥ B.
I urge the reader to pause for a moment and reflect on the significance of this. There is no other way in which concurrent execution can happen at run-time. From a run-time perspective, concurrency is elementary.
From a design-time perspective, things are slightly more involved, but still simple. At design-time, we want to express constraints that would limit the behaviour at run-time. There are four simple constraints that immediately follow from the run-time possibilities:
- A < B
- B < A
- neither A < B, nor B < A; we denote this by A ∥ B,
- either A < B, or B < A; we call this mutually exclusive and we denote this by A ∦ B.
Besides these simple constraints, we should also define conditional concurrency, ℂ (c, A, B), which expands to either A ∥ B or A ∦ B, depending on the run-time evaluation of the expression c. And, of course, we need to expand our schema to include more than two work items; this expansion is trivially achievable.
If we want local reasoning or structured programming, then we should strive to make the concurrency constraints local to different functions. In this case, we would use the simple constraints, and conditional concurrency is not as useful.
In the context of programming languages, the goal of concurrency is to allow the programmer to express concurrency constraints on how different work items need to be executed. These constraints just put bounds on the execution; they still allow a multitude of ways in which work items can be executed.
Expressing concurrency in C++
Let’s now try to express these rules in C++. Let’s assume that A and B are local work items (i.e., that needs to be executed in the body of a function). We will encode them by using function calls.
For the first two cases, it’s easy, as we already have support from the language:
A() ; B()
or
B() ; A()
There is nothing special here; we just sequence the work items in the order we execute them.
Expressing mutual exclusion with local work items is trivial. We choose which one we want to be before the other, and just code it like that. Thus, both A() ; B() and B(); A() are good forms of mutual exclusion between A and B.
To express concurrent execution, we introduce a new abstraction that can be implemented as a function taking a lambda as an argument. The code in Listing 1 shows an example.
A();
auto future = spawn([] { C(); });
B();
future.await();
D();
|
| Listing 1 |
In this example, we express the following concurrency constraints: A < B, A < C, B ∥ C, B < D, and C < D.
The code behaves as if we spawn a new thread to execute C, and then join that thread when awaiting. Of course, we are not doing this, but having that as a mental model might help.
The spawn function returns a future object that is neither movable nor copyable. We will discuss this restriction and alternatives later; for now, it’s important to note that it implies that we only represent local concurrency constraints.
This spawn/await model is similar to other async/await models [Wikipedia-1], but the implementation details differ.
This forms the basis of the concurrency we need.
More examples
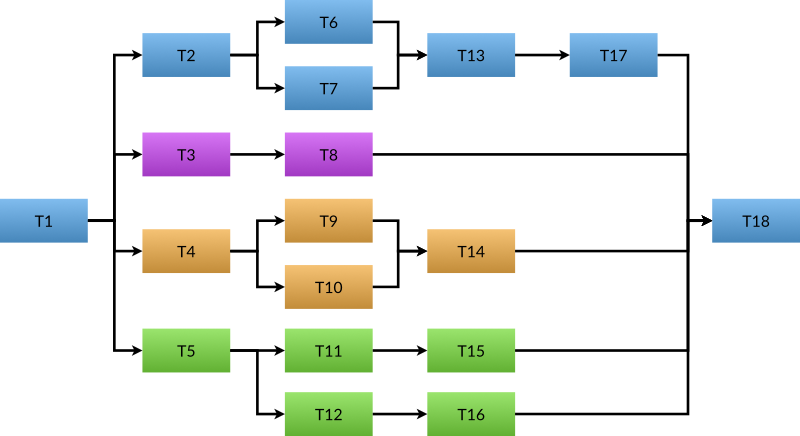
Let’s start with an example showing that this model can be used to encode more complex graphs. Please refer to Listing 2 for an implementation of the graph expressed in Figure 1.
int run_work() {
auto sum = 0;
// T1 is run before anything else.
sum += run_task(1);
// Flow that executes T2, T6, T13, T17.
auto f1 = concore2full::spawn([] {
auto local_sum = 0;
local_sum += run_task(2);
// T6 and T7 are run concurrently.
auto f = concore2full::spawn([] {
return run_task(7); });
local_sum += run_task(6);
local_sum += f.await();
local_sum += run_task(13);
local_sum += run_task(17);
return local_sum;
});
// Flow that executes T3, T8.
auto f2 = concore2full::spawn([] {
return run_task(3) + run_task(8);
});
// Flow that executes T4, T9, T10, T14.
auto f3 = concore2full::spawn([] {
auto local_sum = 0;
local_sum += run_task(4);
// T9 and T10 are run concurrently.
auto f = concore2full::spawn([] {
return run_task(10); });
local_sum += run_task(9);
local_sum += f.await();
local_sum += run_task(14);
return local_sum;
});
// Flow that executes T5, T11, T12, T15, T16.
auto f4 = concore2full::spawn([] {
auto local_sum = 0;
local_sum += run_task(5);
// T11+T15 and T12+T16 are run concurrently.
auto f = concore2full::spawn([] {
return run_task(12) + run_task(16); });
local_sum += run_task(11) + run_task(15);
local_sum += f.await();
return local_sum;
});
// Everything must finish before executing T18.
sum += f1.await() + f2.await() + f3.await()
+ f4.await();
sum += run_task(18);
return sum;
}
|
| Listing 2 |
 |
| Figure 1 |
To build a concurrent sort with this spawn primitive, we can write something similar to Listing 3. In this example, we partition the array that needs to be sorted into two parts so that all the elements on the left side are smaller than the elements on the right side. Then, we can sort the left side and the right side concurrently. This process is recursively applied until the array that needs to be sorted is small enough that a serial sort is more efficient.
template <std::random_access_iterator It>
void concurrent_sort(It first, It last) {
auto size = std::distance(first, last);
if (size_t(size) < size_threshold) {
// Use serial sort under a certain threshold.
std::sort(first, last);
} else {
// Partition the data, such as elements
// [0, mid) < [mid] <= [mid+1, n).
auto p = sort_partition(first, last);
auto mid1 = p.first;
auto mid2 = p.second;
// Spawn work to sort the right-hand side.
auto handle = spawn([=] { concurrent_sort(mid2, last); });
// Execute the sorting on the left side,
// on the current thread.
concurrent_sort(first, mid1);
// We are done when both sides are done.
handle.await();
}
}
|
| Listing 3 |
Listing 4 shows how one can use bulk_spawn to run the computation for a Mandelbrot set concurrently. This primitive spawns multiple work items concurrently, where the number of work items is known at run-time.
void concurrent_mandelbrot(int* vals, int max_x,
int max_y, int depth) {
concore2full::bulk_spawn(max_y, [=](int y) {
for (int x = 0; x < max_x; x++) {
vals[y * max_x + x] =
mandelbrot_core(transform(x, y), depth);
}
}).await();
}
|
| Listing 4 |
This section shows that, using this model, one can build concurrency into slightly more complex problems in an intuitive manner.
Structured concurrency
Let us start by reminding the reader about structured programming. Following the Structured Programming book by Dahl, Dijkstra, and Hoare [Dahl72], we extract two important characteristics of structured programming (there are more, but we are just going to focus on these two).
The first one is the idea that every operation needs to have a single entry and a single exit point. All the basic operations have this shape; the if, while, and for blocks all share this as well. Function calls also have this shape. This makes all the operations in the program have the same shape.
A second significant idea in structured programming is that of recursive decomposition. Complex functionalities can be decomposed into smaller functionalities, which may be further divided into even smaller functionalities. The entire program can be divided into small operations that will ultimately reach the basic operations of the language (variable declaration, assignment, arithmetic operations, etc.).
It’s not enough to just be able to decompose programs into smaller operations; these operations also need to be (to a large degree) independent. That is, one can look at one function and reason about it independently without needing to know how other (unrelated) functions in the program are implemented. Of course, there are interactions between the functions, but these interactions should be reduced as much as possible.
The purpose of structured programming is to enable local reasoning. As Dijkstra puts it, the human mind is limited. Having a linear flow in the program, in which every operation has the same shape, and being able to recursively decompose the program into smaller, mostly independent chunks, helps our mind reason about the code.
Let’s now turn our attention to the properties of the future. A future can be of four types, based on the movability and copyability traits:
- not movable and not copyable (what we’ve seen above)
- movable but not copyable
- movable and copyable
- not movable but copyable
The last option doesn’t make much sense, and we can drop it. Thus, we have only three options to analyse. The most restrictive one is for the future to be not movable and not copyable.
Not being able to move the future implies that the await call (we always assume that there will be an await call) needs to be in the same scope as the spawn. This means that the pair spawn/await can behave like a block (there are some exceptions, but we can safely ignore those). Such a block has one entry and one exit point. This means that using spawn/await blocks follows the idea of structured programming.
With this type of future, we can say that we obtain structured concurrency. It makes it easy to reason about concurrency, localising the concurrency concerns, and allowing for their encapsulation.
Now, because the await is in the same scope as spawn, it means that the stack used at the spawn point is kept alive until await. However, because the spawned work needs to be completed before await, it follows that the spawn work can safely access the stack available at the spawn point. In the example for Listing 1, both B() and C() can access the stack that was available at the call of A().
Furthermore, we can store directly in the future object all the data needed to synchronise between the two work items that need to be executed concurrently. This helps performance, as there is no need for a heap allocation.
While this future type is more restrictive than the others, it clearly provides advantages.
Let us now look at the future that is movable (but still not copyable). Listing 5 provides an example of using such a future.
auto spawn_work() {
A();
std::vector<int> data;
return escaping_spawn([] {
C();
});
}
void weakly_structured_concurrency() {
auto future = spawn_work();
B();
future.await();
D();
}
|
| Listing 5 |
In this example, we use a different abstraction, called escaping_spawn, as we need to produce a different type of future. We see that the spawn point and the await point happen at different points, and for that reason, the concurrency model is not fully structured. We call this model weakly structured concurrency.
While the guarantees for this style are weaker, one can still reason about the concurrency being handled between the two functions. The declaration of the spawn_work() function indicates that we are escaping a future. Reasoning about such an escaped function is similar to that needed for returned functors.
If we look at the stack access, we notice that, in this case, C() cannot access the stack at point A() (for example, access the data variable). The spawn_work function might exit before C() gets a chance to execute. The spawned work can only access stack data that is kept alive by the await call. However, because we require global reasoning to understand where the await point is, in most cases the spawned work cannot access the stack from which it was spawned.
Similarly, we cannot put the data required for the synchronisation on the stack, as the stack may shortly disappear. Thus, we need to have a heap allocation for escaping_spawn.
Thus, weakly structured concurrency is less restrictive, but is not as efficient. This is another example that shows that, sometimes, adding restrictions in a language may provide additional guarantees, improving it. In this case, not being able to move a future allows us to use the stack at the spawn point, and allows improved performance.
The bulk_spawn abstraction that we’ve seen in Listing 4, can work both in strict structured concurrency but also in weak concurrency cases. For bulk_spawn we allocate the frame object on the heap, as the size of the frame depends on run-time parameters.
At the point of writing this article, we haven’t yet implemented copyable futures; their implementation is more involved, as one spawned work item can potentially continue multiple flows that await the result of the original work item.
Implementing spawn
Now that we have described the expectations around using this model, let us describe how this can be implemented. We are going to focus on the implementation of spawn, but the implementation of escaping_spawn and bulk_spawn is similar. We use the code from Listing 1 as our running example.
First, we are using a task pool to handle the spawned work. This is a pretty common technique.
Now, if the work B() takes more time than the work C(), then the execution follows the expected pattern; please see Figure 2. There would be no blocking wait. The original thread would execute A(), then B(), then D(), while a worker thread would execute C(). The work corresponding to C() would finish before the await point, thus all the concurrent constraints are satisfied. All good.
 |
| Figure 2 |
The problem appears if executing C() takes longer than executing B(). The original thread arrives at the await point before the work corresponding to C() is complete. This means that the original thread cannot continue executing D(); see Figure 3.
 |
| Figure 3 |
A common strategy is to block the thread until C() is done. However, this has negative performance implications. We cannot go this route (at least, not for the general case).
Another strategy is for the original thread to steal some other work from the system and execute it while waiting for C() to complete. However, while this strategy keeps throughput of the application high, it has negative implications in terms of latency. For example, if C() is 500μs longer than B(), we might start another work item that takes 1s to execute. So, we introduce a latency of 1s into this thread. This is not a good strategy either.
A better strategy is to let the worker thread continue executing work D(), instead of executing it on the original thread. A similar strategy is employed by the when_all() algorithm from senders/receivers [P2300R9]. If we do this, a new challenge arises: what can the original thread do in the meantime?
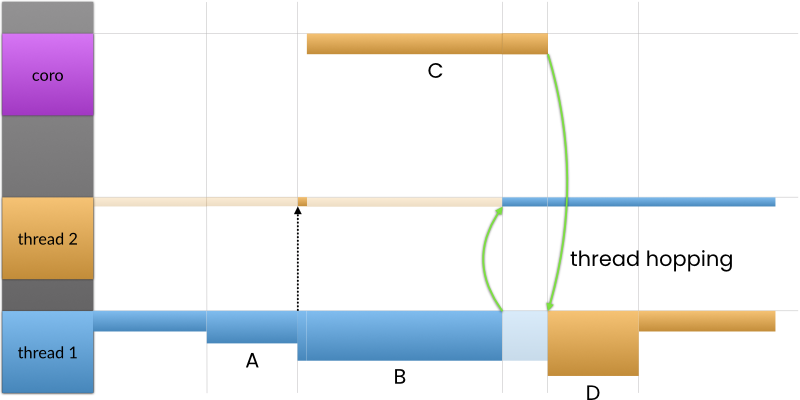
Well, this may be a bit counterintuitive to the reader, but an adequate option is to go to the thread pool and continue the work there. That is, we essentially switch the threads. The original thread will continue to execute whatever the worker thread has, while the worker thread will continue to execute everything on the main flow after the await point. We also call this behaviour thread hopping.
A simplified view of a thread is that it consists of a set of registers (most importantly an instruction pointer, IP, and a stack pointer, SP) plus a stack memory region associated with it. During the lifetime of the thread, the stack pointer register keeps changing within the stack region. Thread hopping essentially swaps important registers between threads, allowing a thread to point to the stack region created by another thread.
A good technique to implement thread hopping is to use stackful coroutines [Moura09]. Indeed, for my implementation, I’ve used the boost::context library [context]. A stackful coroutine is created to execute the spawned work; the worker thread doesn’t do much work on its stack, as it immediately jumps to the coroutine stack.
Figure 4 shows how thread hopping works. On the left side of the figure, we depict the stack regions; we have three of them: two for the threads and one for the coroutine that was created. After executing B() thread 1 jumps and continues execution on the stack created for thread 2. After executing C(), thread 2 continues to execute the continuation on the stack created for thread 1. At the end of the work, the two threads are essentially swapped.
 |
| Figure 4 |
There is another case that needs to be discussed. It might happen that, during the entire execution of the work, there isn’t a worker thread available to execute the C() work item. If, when reaching the await point, the task corresponding to C() has not been taken by a worker thread for execution, we execute it inline, on the original thread.
It is important to note that this execution is consistent with the concurrency constraints. That is, B < C can be a valid execution of B ∥ C, and we still have B < D and C < D.
In this case, we don’t create a new coroutine for executing C(). We are doing the most reasonable thing to do in the case where we don’t have enough hardware resources.
Allowing thread switching, we ensure that in any scenario, the system will not block, and we always execute work items as soon as possible, within the bounds of the given concurrency constraints.
A direct consequence of thread hopping is that a function may enter on one thread and exit on a different thread. Please note that this still respects the principles of structured programming.
Similar to spawn, we can implement escaping_spawn (to create weakly structured futures) and bulk_spawn (to start executing multiple work items at the same time).
Early measurements
The ideas presented here are still a work-in-progress. But, even in this case, a few measurements would help to understand whether the direction in which this is moving is promising or not.
Skynet
Let’s start with the Skynet micro-benchmark [Skynet]. We create a task, which creates 10 more tasks, each creating 10 more tasks, etc. At the final level, we would be creating 10 million tasks (original benchmark was going up to 1 million, but we increased it to 10 million). The tasks at the final level are returning their ordinal number, while the other tasks are just summing up the values returned from the children. In total, there are five quadrillion five trillion tasks created.
The purpose of this micro-benchmark is to check if the task model scales for a massive number of tasks. We check whether the program deadlocks or we run out of stack or other resources. In terms of performance, this will measure the overhead of creating and joining tasks, and it’s not very representative of real-world workloads (where we would do more useful work, and create fewer tasks).
The results of running this micro-benchmark are presented in Figure 5. First, we present the ‘reference’ measurements, that is, the implementation of the micro-benchmark in Go, which uses concurrency with goroutines.
 |
| Figure 5 |
Next, we present the measurements corresponding to three C++ implementations: one that just uses coroutines, one that uses senders/receivers and coroutines, and one that uses senders/receivers and the sync_wait algorithm. The coroutine version is single-threaded. The version that uses senders/receivers with a coroutine task uses a thread pool and fully utilises all the cores on the machine; it achieves the best performance from all our measurements. It is important to note that the version with sync_wait deadlocks as soon as it creates more tasks than there are threads in the thread pool.
Then we show the measurements made for our concurrency framework in three different scenarios: using structured concurrency (spawn), using weakly structured concurrency (escaping_spawn), and spawning 10 items at once (bulk_spawn). All three measurements corresponding to our implementation are faster than the Go implementation. The spawn execution is 20% slower than the senders/receivers execution. As expected, the structured concurrency program is faster than the other two versions. In the weakly structured concurrency, we are doing a heap allocation for each work item we spawn, while in the case of bulk spawning items, we are making a heap allocation for spawning the work for 10 children.
The results from running this micro-benchmark are overall positive. Firstly, we did not deadlock (unlike the sync_wait version), and we did not consume a large amount of stack. In terms of performance, we are 20% slower than the fastest version measured. This result is not that bad, considering the overhead is relatively small, and that the number of spawn/await points in a typical application is relatively small.
Speedup
Another micro-benchmark worth doing is checking the scale-up of a somewhat more realistic problem (computing the Mandelbrot values for a 4K image, one task per row). This time, we try to specify the number of threads that the library can use and measure the total runtime.
Figure 6 shows the speedup results for running this on my Apple MacBook Pro, M2 Pro, 16 GB, with 12 cores (8 performance, 4 efficiency); the total execution time for a test is between 868 ms and 9319 ms. The speedup looks really good; for up to 8 threads, it is really close to the ideal numbers. Going between 8 and 12 threads, the speedup is not that great, as we are utilising the efficiency cores for performance tasks. Going past 12, the number of cores on my machine, doesn’t help; there are simply no extra resources to speed up the computation.
 |
| Figure 6 |
For people familiar with speedup calculations, the numbers are excellent.
Analysis
Expressing concurrency
The concurrency model presented here is very good at expressing concurrency. With just a few primitives, we are able to represent many concurrency problems. While we don’t have conditional concurrency implemented yet, many problems do not need it directly (expressing non-local concurrency constraints is not best practice).
The model provides a forward progress guarantee. Once a work item starts executing, it will complete and, eventually, all work items are started. Thus, all the spawned work items are executed. This means that the program will always make progress and never be stuck.
Safety
The model assumes that the user ensures proper constraints between work items. That is, there are no two concurrent tasks that access the same memory location such that at least one of them is writing to it. This forms a basic precondition of writing a concurrent relationship between work items. If this precondition is met, the model doesn’t have any race conditions.
The model allows directly expressing concurrency constraints, so there is no need for extra synchronisation; this eliminates an entire category of safety issues. In particular, there are no deadlocks.
To conclude, if the constraints are correctly set, the model ensures concurrency safety.
Performance
The concurrency model that we presented doesn’t require blocking waits at the user level. This is a huge performance advantage compared to many other models found in practice. The only performance costs that the model incurs are localised in the calls to spawn and await. As we’ve seen, early measurements indicate that this makes the model about 20% slower compared to the implementation on top of senders/receivers. This is a good number in itself.
In real-world applications, the time spent in spawn/await is tiny compared to the useful work. This means that this 20% will not affect the overall performance of these applications. This can be seen from the speedup measurements we’ve presented.
To conclude, the performance appears to be good, but not necessarily the best.
Stack usage
In general, there is a concern that models based on stackful coroutines are bad because of their stack usage. That is, one cannot spawn too many coroutines as it would require many stack allocations, each coroutine needing a full stack. The results from the Skynet micro-benchmark proved that our model doesn’t have this problem.
An important factor that influences stack consumption is the way we create a coroutine stack for spawning new work: we only do that after creating a task in our thread pool. This means that the number of coroutine stacks used for spawning work is limited by the number of threads in the thread pool.
At this point, the implementation of the model also creates a coroutine inside await, to be able to swap continuations. The stack requirements for this one are small, and, with a bit of extra work, can be avoided (e.g., by reusing the caller’s stack).
Furthermore, the worker threads don’t need a lot of stack space. They would only jump to executing on coroutine stacks.
All these, with some extra tuning, can make the stack usage of this concurrency model to be small. It can be smaller than the stack required for an application that uses the threads-and-locks model and creates more threads than necessary.
Interoperability
Here, the model doesn’t fare that well. The main reason is that, with thread hopping, a function execution can start on one thread and end on a different one. This may break the assumptions of the surrounding code.
If external code calls into our code that uses thread hopping, it may need to restore the original thread each time it calls a function into our code. This potentially involves a blocking wait (the original thread may be doing something else, and we need to wait for it to finish). This is not great.
Additionally, the code cannot use thread-local storage in the way people are accustomed to.
These interoperability challenges are present in all asynchronous models (senders/receivers, other async/await models). In each of these models, there needs to be a synchronous-wait operation so that synchronous code can call asynchronous code.
More to explore
The current implementation of the model is still young. More features need to be added to it. We need copyable futures, so that multiple parties can await the completion of a work item. Then, we have to add cancellation to the entire model.
To be able to easily encode non-local concurrency constraints, we also need more support for what we call conditional concurrency: that is, sometimes work items are executed concurrently, sometimes they are mutually exclusive, depending on some other conditions.
Another important aspect that we should consider is the integration with I/O, timers, running work on GPUs, and custom execution contexts.
All these are in the plan for the future of the model.
Conclusions
We presented a model for concurrency that starts from the theory and tries to put it into practice in a simple, easy-to-reason-about, and efficient way.
The theory of concurrency is surprisingly simple: just partial ordering on the execution of work items. Instead of modelling this concurrency with mutexes, semaphores, and other synchronisation primitives, we can directly try to express the possible constraints in the code. We introduce the spawn/await model, which can model the most common concurrency constraints.
Using spawn/await will keep us in the realm of structured programming. The spawn/await block can be considered an operation with one entry and one exit point, so it has a similar shape to the rest of the operations. We can still use recursive decomposition, and we can encapsulate concurrency constraints inside functions. For example, we might add concurrent execution to a function that previously did not have any, without the callers being affected by it.
All this makes the model give us reasonable concurrency. That is, something that we can easily reason about, and something that is not out-of-ordinary, something that is not unexpected, outrageous, or excessively costly. One doesn’t need to use dark arts to master concurrency.
References
[concore2full] Lucian Radu Teodorescu, concore2full library, https://github.com/hylo-lang/concore2full, accessed April 2024.
[context] Oliver Kowalke, boost::context library, https://www.boost.org/doc/libs/1_85_0/libs/context/.
[Dahl72] O.-J. Dahl, E. W. Dijkstra, C. A. R. Hoare, Structured Programming, Academic Press Ltd., 1972.
[Hoare14] Tony Hoare, Stephan van Staden, The laws of programming unify process calculi, Science of Computer Programming 85, 2014.
[Hylo] The Hylo Programming Language, https://www.hylo-lang.org/.
[Moura09] Ana Lúcia De Moura, Roberto Ierusalimschy, Revisiting coroutines, ACM Transactions on Programming Languages and Systems (TOPLAS), 2009, https://dl.acm.org/doi/pdf/10.1145/1462166.1462167.
[Nystrom15] Bob Nystrom, What Color is Your Function?, https://journal.stuffwithstuff.com/2015/02/01/what-color-is-your-function/.
[P2300R9] Michał Dominiak, Georgy Evtushenko, Lewis Baker, Lucian Radu Teodorescu, Lee Howes, Kirk Shoop, Michael Garland, Eric Niebler, Bryce Adelstein Lelbach, std::execution, 2024, http://wg21.link/P2300R9.
[Skynet] Alexander Temerev, Skynet 1M concurrency microbenchmark, https://github.com/atemerev/skynet.
[Teodorescu24] Lucian Radu Teodorescu, Concurrency Hylomorphism, ACCU Conference, April 2024, https://www.youtube.com/watch?v=k6fI4asLJxo.
[Wikipedia-1] Wikipedia, Async/await, https://en.wikipedia.org/wiki/Async/await, 2024.
[Wikipedia-2] Wikipedia, Out-of-order execution, https://en.wikipedia.org/wiki/Out-of-order_execution, 2024.
has a PhD in programming languages and is a Staff Engineer at Garmin. He likes challenges; and understanding the essence of things (if there is one) constitutes the biggest challenge of all.











