Unordered maps can be implemented in various ways. Joaquín M López Muñoz presents a new, fast version.
Several Boost authors have embarked on a project [Boost-1] to improve the performance of Boost.Unordered’s implementation of std::unordered_map (and multimap, set and multiset variants), and to extend its portfolio of available containers to offer faster, non-standard alternatives based on open addressing.
The first goal of the project has been completed in time for Boost 1.80 (launching in August 2022). We describe here the technical innovations introduced in boost::unordered_map that makes it the fastest implementation of std::unordered_map on the market.
Closed vs. open addressing
On a first approximation, hash table implementations fall on either of two general classes:
- Closed addressing (also known as separate chaining [Wikipedia-1]) relies on an array of buckets, each of which points to a list of elements belonging to it. When a new element goes to an already occupied bucket, it is simply linked to the associated element list. Figure 1 depicts what we call the textbook implementation of closed addressing, arguably the simplest layout, and among the fastest, for this type of hash tables.
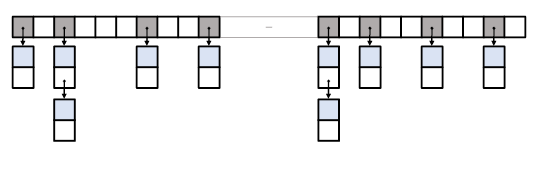
Figure 1 - Open addressing [Wikipedia-2] (or closed hashing) stores at most one element in each bucket (sometimes called a slot). When an element goes to an already occupied slot, some probing mechanism is used to locate an available slot, preferrably close to the original one.
Recent, high-performance hash tables use open addressing and leverage on its inherently better cache locality and on widely available SIMD [Wikpedia-3] operations. Closed addressing provides some functional advantages, though, and remains relevant as the required foundation for the implementation of std::unodered_map.
Restrictions on the implementation of std::unordered_map
The standardization of C++ unordered associative containers is based on Matt Austern’s 2003 N1456 paper [Austern03]. Back in the day, open-addressing approaches were not regarded as sufficiently mature, so closed addressing was taken as the safe implementation of choice. Even though the C++ standard does not explicitly require that closed addressing must be used, the assumption that this is the case leaks through the public interface of std::unordered_map:
- A bucket API is provided.
- Pointer stability implies that the container is node-based. In C++17, this implication was made explicit with the introduction of
extractcapabilities. - Users can control the container load factor.
- Requirements on the hash function are very lax (open addressing depends on high-quality hash functions with the ability to spread keys widely across the space of
std::size_tvalues.)
As a result, all standard library implementations use some form of closed addressing for the internal structure of their std::unordered_map (and related containers).
Coming as an additional difficulty, there are two complexity requirements:
- iterator increment must be (amortized) constant time,
erasemust be constant time on average,
that rule out the textbook implementation of closed addressing (see N2023 [López-Muñoz06] for details). To cope with this problem, standard libraries depart from the textbook layout in ways that introduce speed and memory penalties: for instance, Figure 2 shows how libstdc++-v3 and libc++ layouts look.
 |
| Figure 2 |
To provide constant iterator increment, all nodes are linked together, which in its turn forces two adjustments to the data structure:
- Buckets point to the node before the first one in the bucket so as to preserve constant-time erasure.
- To detect the end of a bucket, the element hash value is added as a data member of the node itself (libstdc++-v3 opts for on-the-fly hash calculation under some circumstances).
Visual Studio standard library (formerly from Dinkumware) uses an entirely different approach to circumvent the problem, but the general outcome is that resulting data structures perform significantly worse than the textbook layout in terms of speed, memory consumption, or both.
Boost.Unordered 1.80 data layout
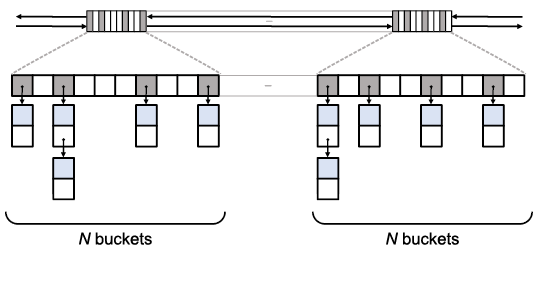
The new data layout used by Boost.Unordered goes back to the textbook approach (see Figure 3).
 |
| Figure 3 |
Unlike the rest of standard library implementations, nodes are not linked across the container but only within each bucket. This makes constant-time erase trivially implementable, but leaves unsolved the problem of constant-time iterator increment: to achieve it, we introduce so-called bucket groups (top of the diagram). Each bucket group consists of a 32/64-bit bucket occupancy mask plus next and prev pointers linking non-empty bucket groups together. Iteration across buckets resorts to a combination of bit manipulation operations on the bitmasks plus group traversal through next pointers, which is not only constant time but also very lightweight in terms of execution time and of memory overhead (4 bits per bucket).
Fast modulo
When inserting or looking for an element, hash table implementations need to map the element hash value into the array of buckets (or slots in the open-addressing case). There are two general approaches in common use:
- Bucket array sizes follow a sequence of prime numbers p, and mapping is of the form h → h mod p.
- Bucket array sizes follow a power-of-two sequence 2n, and mapping takes n bits from h. Typically it is the n least significant bits that are used, but in some cases, like when h is postprocessed to improve its uniformity via multiplication by a well-chosen constant m (such as defined by Fibonacci hashing [Wikipedia-4]), it is best to take the n most significant bits, that is, h → (h × m) >> (N − n), where N is the bitwidth of
std::size_tand>>is the usual C++ right shift operation.
We use the modulo by a prime approach because it produces very good spreading even if hash values are not uniformly distributed. In modern CPUs, however, modulo is an expensive operation involving integer division; compilers, on the other hand, know how to perform modulo by a constant much more efficiently, so one possible optimization is to keep a table of pointers to functions fp : h → h mod p. This technique replaces expensive modulo calculation with a table jump plus a modulo-by-a-constant operation.
In Boost.Unordered 1.80, we have gone a step further. Daniel Lemire et al. [Lemire19] show how to calculate h mod p as an operation involving some shifts and multiplications by p and a pre-computed c value acting as a sort of reciprocal of p. We have used this work to implement hash mapping as h → fastmod(h, p, c) (some details omitted). Note that, even though fastmod is generally faster than modulo by a constant, most performance gains actually come from the fact that we are eliminating the table jump needed to select fp, which prevented code inlining.
Time and memory performance of Boost 1.80 boost::unordered_map
We are providing some benchmark results [Boost-2] of the boost::unordered_map against libstdc++-v3, libc++ and Visual Studio standard library for insertion, lookup and erasure scenarios. boost::unordered_map is mostly faster across the board, and in some cases significantly so. There are three factors contributing to this performance advantage:
- the very reduced memory footprint improves cache utilization,
- fast modulo is used,
- the new layout incurs one less pointer indirection than libstdc++-v3 and libc++ to access the elements of a bucket.
As for memory consumption, let N be the number of elements in a container with B buckets: the memory overheads (that is, memory allocated minus memory used strictly for the elements themselves) of the different implementations on 64-bit architectures are in Table 1.
|
|||||||||||
| Table 1 |
Which hash container to choose
Opting for closed-addressing (which, in the realm of C++, is almost synonymous with using an implementation of std::unordered_map) or choosing a speed-oriented, open-addressing container is in practice not a clear-cut decision. Some factors favoring one or the other option are listed:
std::unordered_map- The code uses some specific parts of its API-like node extraction, the bucket interface or the ability to set the maximum load factor, which are generally not available in open-addressing containers.
- Pointer stability and/or non-moveability of values required (though some open-addressing alternatives support these at the expense of reduced performance).
- Constant-time iterator increment required.
- Hash functions used are only mid-quality (open addressing requires that the hash function have very good key-spreading properties).
- Equivalent key support, i.e.
unordered_multimap/unordered_multiset, required. We do not know of any open-addressing container supporting equivalent keys.
- Open-addressing containers
- Performance is the main concern.
- Existing code can be adapted to a basically more stringent API and more demanding requirements on the element type (like moveability).
- Hash functions are of good quality (or the default ones from the container provider are used).
If you decide to use std::unordered_map, Boost.Unordered 1.80 now gives you the fastest, fully-conformant implementation on the market.
Next steps
There are some further areas of improvement to boost::unordered_map that we will investigate post Boost 1.80:
- Reduce the memory overhead of the new layout from 4 bits to 3 bits per bucket.
- Speed up performance for equivalent key variants (
unordered_multimap/unordered_multiset).
In parallel, we are working on the future boost::unordered_flat_map, our proposal for a top-speed, open-addressing container beyond the limitations imposed by std::unordered_map interface. Your feedback on our current and future work is very welcome.
Acknowledgements
The Boost.Unordered evolution project is being carried out by Peter Dimov, Christian Mazakas and the author. This work is funded by The C++ Alliance (https://cppalliance.org/).
References
[Austern03] ‘A Proposal to Add Hash Tables to the Standard Library (revision 4)’: https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2003/n1456.html
[Boost-1] ‘Development Plan for Boost.Unordered’:
https://pdimov.github.io/articles/unordered_dev_plan.html
[Boost-2] ‘Benchmarks’: https://www.boost.org/doc/libs/develop/libs/unordered/doc/html/unordered.html#benchmarks
[GNU] ‘Hash Code’ in The GNU C++ Library Manual, available at https://gcc.gnu.org/onlinedocs/libstdc++/manual/unordered_associative.html#containers.unordered.cache
[Lemire19] Daniel Lemire, Owen Kaser and Nathan Kurz, ‘Faster Remainder by Direct Computation: Applications to ompilers and Sofware Libraries’ from Software: Practice and Experience 49(6), available at https://arxiv.org/abs/1902.01961
[López-Muñoz06] ‘erase (iterator) for unordered containers should not return an iterator’: https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2006/n2023.pdf
[Wikipedia-1] ‘Separate chaining’ in the topic ‘Hash table’:
https://en.wikipedia.org/wiki/Hash_table#Separate_chaining
[Wikipedia-2] ‘Open addressing’ in the topic ‘Hash table’:
https://en.wikipedia.org/wiki/Hash_table#Open_addressing
[Wikipedia-3] ‘Single instruction, multiple data’:
https://en.wikipedia.org/wiki/Single_instruction,_multiple_data
[Wikipedia-4] ‘Fibonacci hashing’ in the topic ‘Hash table’
https://en.wikipedia.org/wiki/Hash_function#Fibonacci_hashing
This article was first published on Joaquín’s blog Bannalia: trivial notes on themes diverse (http://bannalia.blogspot.com/2022/06/advancing-state-of-art-for.html?m=1) on 18 June 2022.
is a telecommunications engineer freelancing in product/innovation/technological consultancy for telco, TV, and IoT. He is the author of three Boost libraries (MultiIndex, Flyweight, PolyCollection) and has made some minor contributions to the standard, such as N3657 (heterogeneous lookup).











