Don’t Block Doors

Being in lockdown for much of the last couple of years, many of us feel a bit anxious about being in crowded spaces. You’ve probably seen models of how a pandemic spreads; those are fairly common. For my presentation at the ACCU conference in April, I used cellular automata to create some models. Instead of modeling the spread of a disease, I started from first principles – people moving in space. If we wanted to see how an infection spreads through a crowd, we could extend this example.

In this article, you’ll learn how to make a simple cellular automata (CA) model. CAs date back to the 1940s and were introduced by von Neumann [Wikipedia-1], among others. People had grand ideas of sending robots into space to mine precious metals and wondered if the robots could be autonomous and even repair or rebuild themselves. This need for robot autonomy lead to a simplified idea of minimal units or cells following instructions – CA were born. They have tended to remain a bit of a niche curiosity; however, CAs can be used to model aspects of biology from patterns on shells to fibroblasts. You can also use them to model fluid flows [Wikipedia-2]. Whatever your motivation, CAs are surprisingly simple to code up and fun to watch.

People moving in space

Let’s build a simple CA to model people moving in space. We can then watch what happens and see if we learn anything. We’ll model the world as a two-dimensional space containing some blobs. The blobs start inside a paper bag and can move around. As a bonus, if the blobs manage to get out of the bag, we’ve coded our way out of a paper bag, which is a useful skill. The blobs could represent conference attendees moving through an atrium, represented by the bag. Maybe the attendees are heading to the bar or outside. We could make many possible simulations, but the simplest is to see the space as a grid (Figure 1).

Figure 1

Each circle is a space a blob can occupy. All but the top row are in the paper bag/atrium – whatever we are modelling. The top row is outside the paper bag, simulating people moving outside an enclosed space, and arriving in the bar or another destination.

It’s easy to vary the number of blobs or their starting positions, but imagine you have a row – maybe people who just left a talk or workshop (Figure 2).

Figure 2

If they all walked forward at the same pace, we would have something very easy to code, but it wouldn’t be much fun to watch and we wouldn’t learn much. Instead, let’s build stochastic cellular automata. Our blobs are the automata – they have agency and can therefore move. They move in the cells, so are cellular in that sense, rather than being living, breathing organisms. Finally, they are stochastic, in the sense that their movements are random.

Starting positions and neighbours

Some cellular automata, such as Conway’s Game of Life [Game-of-Life], have deterministic rules, though may initialize their grids at random. In this article, we’ve doing things the other way round: always placing the automata in the same starting position, but letting them make random moves. Rather than teleporting off to another cell, each automaton can only move only to an adjacent or neighboring square. In general, cellular automata tend to use one of two definitions of ‘neighbour’, von Neumann, or Moore.

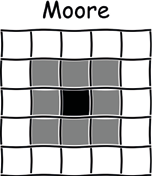
Moore’s schema includes the eight surrounding squares, up, down, left, right and the diagonals. Von Neumann’s is the simplest, since it has only four, up, down, left, and right with no diagonals. Let’s keep it simple.

Defining movement

So, we know where the blobs start, and where they can move to. Let’s stop them from going through the sides or standing on each other, so the four neighboring cells may not be available. Let’s also allow a blob to stay still if it chooses.

In order to make the cellular automata stochastic, we simply pick a possible, allowed move at random. For example, given a some possible moves, in C++ you form a new list of unoccupied positions:

  std::vector<std::pair<int, int>> moves{{0, 0},
    {-1, 0}, {1, 0}, {0, 1}, {0, -1}};

Feel free to use a language of your choice.

The first number is a step left or right; -1 or 1 respectively. The second indicates up or down. {0, 0} means the blob stays still. Now, we could pick any of these options; however, if any move is equally likely, the blobs will amble around for a long time. If our attendees are aiming to escape the paper bag, we can encourage them to go up. Only one of the options involves up, {0, 1}, so making that combination more likely gives us what we need.

More complex options

You can do more sophisticated things, and then build all kinds of simulations. What we have done, in effect, is hard code what’s called a static floor field. It’s static because it doesn’t change, and it’s a floor field because, like a magnetic field or similar, it influences the blobs within it. In this case they tend to go up. We could ascribe weights or values to cells in the grid and use those instead, like this for a door or exit at the top. See Figure 3.

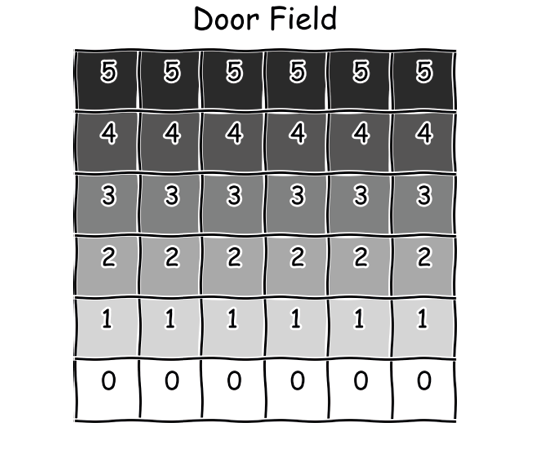Figure 3

That scheme is over the top for this simple case, but would allow us to add obstacles and even have a dynamic floor field if we wanted.

An algorithm to move blobs

Now that we have things to move and know how to choose where they move, the simplest thing to do is let each blob move, one at a time. In theory, you could let them all move together, but you’d have to do something about blobs trying to move to the same grid square. If you make a grid class to keep track of where each blob is, the overall algorithm is as follows:

  choose n (=25)
  put n blobs in grid (at bottom of bag)
  while True:
    draw bag
    for each Blob in grid:
      if blob in bag:
        move blob
    draw blobs

Blobs do gradually move towards the door. Success. However, since there is only one row at the top, they end up blocking the door and the later escapees get stuck – for quite a long time. For example, colouring the blobs in the bag cyan and changing them to magenta when they escape, you can see the escaped blobs partially blocking the door for the others (see Figure 4, and there’s an animated version available [Buontempo22]).

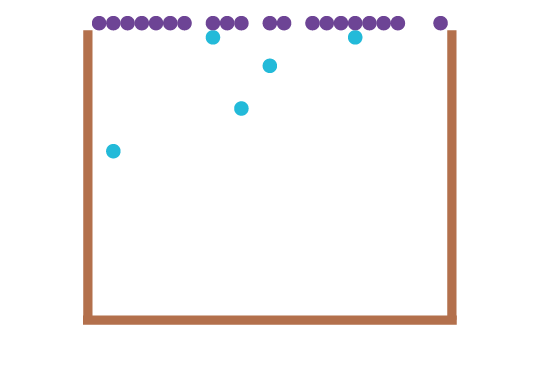Figure 4

A dynamic floor field, simulating the blobs noticing what’s happening around them, might overcome this. After drawing the blobs in the loop, you could increase the field value of empty spaces. This change would encourage Blobs to move away from each other. Alternatively, adding several other rows so there’s more space to move into might help too. This second solutions is akin to encouraging people not to block doorways. Something worth remembering if you’ve not been outside for a while!

Both options are simple to code up, but do tell us important things about crowd control and designing a space. The floor field simulates the directions people tend to move in. If you are trying to leave a conference centre, an airport, or similar, there are exit signs, which are often lit up. The clear signage is meant to encourage people to move in a given direction, which clearly matters in the case of an emergency. Sometimes exits get blocked, so turning those exit signs off, and even introducing a one way system, might get people safely out of a building more quickly. You can then ask yourself what-if questions: what if we add more exit signs; try a one way system; and so on? You can use your simulation to measure the total time taken to evacuate everyone, or find out if some blobs get stuck or even trampled.

CAs are loads of fun. This stochastic cellular automata reminds us not to stand in doorways, but you can use CAs to design a space for safety – and so much more! Have a play with cellular automata. Try some what-if questions. For example, add some obstacles and see what happens.

References

[Buontempo22] Door blocking CA: https://www.youtube.com/watch?v=wlsbg5q0hO0

[Game-of-Life] Game of Life: https://playgameoflife.com/

[Wikipedia-1] Von Newmann cellular automaton: https://en.wikipedia.org/wiki/Von_Neumann_cellular_automaton

[Wikipedia-2] Lattice gas automaton: https://en.wikipedia.org/wiki/Lattice_gas_automaton

This article was first published online on Pragmatic Programmers on 15 June 2022 (https://medium.com/pragmatic-programmers/dont-block-doors-e38e7affbf56). You will find more information in Fran’s ACCU Conference presentation. You may also enjoy Genetic Algorithms and Machine Learning for Programmers, published by The Pragmatic Bookshelf.

Frances Buontempo has a BA in Maths + Philosophy, an MSc in Pure Maths and a PhD technically in Chemical Engineering, but mainly programming and learning about AI and data mining. She has been a programmer since the 90s, and learnt to program by reading the manual for her Dad’s BBC model B machine.