Reading code is time consuming. Lucian Radu Teodorescu takes it one step further and asks how we reason about code.
I think it’s well known in the software industry that we spend more time reading code than writing it. One person who helped popularise this idea is Kevlin Henney. See Figure 1 for two tweets posted by Kevlin arguing this idea [Henney20]. At that point, I also argued that we should probably be using the terms ‘Reasoning’ or ‘Understanding’ instead of ‘Reading’ to reflect more accurately what software developers do when they sit in front of the code.
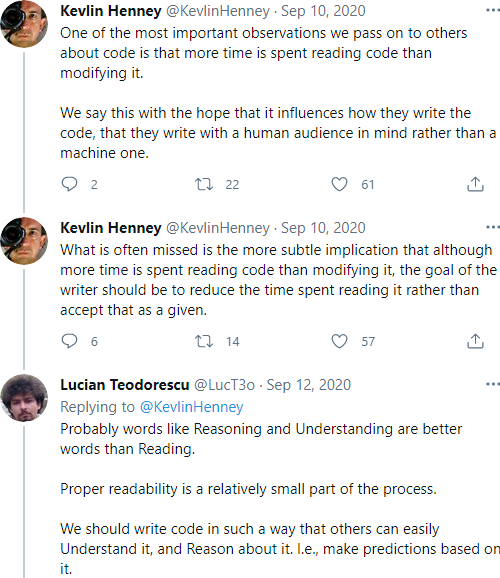 |
| Figure 1 |
Five minutes after posting my tweet, one question found its way into my head, and then dark thoughts followed. What does it mean to Reason about code? After letting these thoughts multiply and form connections in the back of my mind for several months, this article tries to provide an answer to that question.
We will try to find out how proper reasoning about code should be undertaken, and then we will inspect some very interesting implications of our ability to reason about code.
What would proper reasoning mean?
According to the Merriam-Webster dictionary [MW], Reason means (selected entries):
- a rational ground or motive
- a sufficient ground of explanation or of logical defense; especially : something (such as a principle or law) that supports a conclusion or explains a fact
- the power of comprehending, inferring, or thinking especially in orderly rational ways
There are other, softer, meanings of the word Reason, but, as we are in an engineering discipline, we should rely on science; so we will take the most scientific definition we can get.
For this reason, for the rest of the article I will assume that reasoning about the code means to comprehend the code, its exact meaning and its limitations, and to be able to properly draw conclusions about its implications – all done in a logical/mathematical way.
For example, if i is an integer, then reasoning about the statement i++ should include:
- whether the expression is valid
- what would be the value of
iafter the increment - what would be the returned value
- when the new
iwill be higher than the oldi(not always true!) - what happens when we reach the maximum value allowed for the integer type
There are multiple ways of formalising this analysis. One common method used in Software Engineering is by using Hoare rules [Hoare69]. In this formalism, for each command/instruction C we have a set of pre-conditions {P}, and a set of postconditions {Q} – typically represented as a triple {P}C{Q}. If the preconditions {P} hold, then after executing C the postconditions {Q} will also hold.
Therefore, reasoning about a code C means finding out all the properties that belong to the set {Q}. And, of course, by finding out we should mean proving. That is, reasoning about code should mean a process of mathematically proving the implications of the code.
Please note that, in this context, the preconditions {P} and postconditions {Q} refer to mental activities, and have little to do with the definition of the programming language. They refer the set of thoughts that are in our heads, if we were to reason about these mathematically.
This type of reasoning is something that we don’t do daily when programming, but let’s analyse what it entails.
An analysis of for loops
Let us try to analyse the two for loops shown in Listing 1 and Listing 2. The intent of both code fragments is to print the content of vec.
for (auto el: vec) print(el); |
| Listing 1 |
for (int i=0; i<vec.size(); i++) print(vec[i]); |
| Listing 2 |
Before this, let’s make a few simplifying assumptions:
- we assume all the constructs work as specified in the language standard (I’m assuming C++ in this case)
- we assume all the function calls behave like they are intended to, without us needing to analyse the implementation (i.e., using abstractions simplifies reasoning)
- we indulge ourselves not to be extremely formal
In other words, we want to avoid becoming like Principia Mathematica [Whitehead10], where the equality 1 + 1 = 2 was proved only at page 379 of the book.
Let’s also assume the following preconditions are true at the point where the code appears:
- P1: we are targeting a conformant C++11 compiler
- P2: vec has type
std::vector<int>, with usual semantics - P3:
intdenotes a 32-bit integer - P4: the size of the vector is less than 1000 elements
- P5: function
printis defined with the following signature:void print(int)
We will attempt to list all the postconditions for the two cases, without attempting to prove all of them.
Ranged for loop
Postcondition Q11. The syntax of the code in Listing 1 is valid. (This follows from the language specification. This should have been broken down in multiple items, but let’s not try to be overzealous)
Postcondition Q12. The range expression (vec) is semantically valid.
Postcondition Q13. The for loop, if valid, would iterate over all the elements of the given vector. (By the meaning of for-loops as defined by the C++ standard.)
Postcondition Q14. The range declaration (auto el) is semantically valid. (From the language rules, and considering also that range expression is valid.)
Postcondition Q15. el is a variable of type int.
Postcondition Q16. The call print(el) is semantically valid (and prints the value of el).
Postcondition Q17. The for loop is semantically valid. (Consequence of the other preconditions.)
Postcondition Q18. The for loop will print all the values in the given vector. (Consequence of Q13 and Q17.)
We were not extremely formal, but we managed to prove in 8 steps (more accurately, with 8 postconditions) the semantics and the behaviour of the for loop in Listing 1. Thus, reasoning about the code from Listing 1, with the above assumptions, should entail finding and proving these 8 postconditions.
Please note that if we had more complex types in the vector, or we used a reference for the el variable, or if we had had to do implicit conversions, the analysis would have been more complex.
Classic for loop
Let’s now turn our attention to the for loop in Listing 2.
Postcondition Q21. The syntax of the code in Listing 2 is valid.
Postcondition Q22. The init statement (int i=0) is semantically valid. (This should have been broken down, as we should have proved first that the constant 0 is compatible with type int, but again, let’s not be too overzealous.)
Postcondition Q23. i is a variable of type int.
Postcondition Q24. The initial value of i is 0.
Postcondition Q25. The expression vec.size() is valid, and has the type size_t (this again is more complex than stated here, as the return type is a dependent type – but let’s keep things as simple as we can).
Postcondition Q26. The expression i<vec.size() is valid, and has the type bool. (This comes from the fact that there is an operator < defined between int and size_t, with the usual meaning.)
Postcondition Q27. The expression i++ is semantically valid.
Postcondition Q28. The expression vec[i] is semantically valid, well-defined and has the type int, assuming i is in range 0..N, where N-1 is the number of elements in the vector. (To prove this one needs to take into consideration the implicit conversion from int to size_t, consider the multiple function specialisations and consider the constness of vec.)
Postcondition Q29. Assuming that i is in range 0…N, where N-1 is the number of elements in the vector, then the statement print(vec[i]) is semantically valid and well-defined.
Postcondition Q210. Assuming that i is in range 0…N, where N-1 is the number of elements in the vector, then the for loop from Listing 2 is semantically valid and well-defined.
Now, at this point, the reader might think that we are done; compared to the for loop from Listing 1, it’s not even that bad: 10 postconditions instead of 8. But we haven’t dealt yet with the trickiest part: making sure that the code does what we want to do (print all the values in the vector), i.e., something similar to Q18. OK, so let’s tackle that.
Postcondition Q211. Unless i reaches INT_MAX, then i can only monotonically grow. (To prove this we must notice that the only operation that changes i is i++, and this can only increase the value of i, but only if i hasn’t the value of INT_MAX.)
Postcondition Q212. The value of i can only be positive if i never becomes INT_MAX. (Coming from the previous postcondition, coupled with the initialisation value.)
Postcondition Q213. If i is never INT_MAX then i cannot be greater than N, where N is the size of the vector (but can be equal to N).
Postcondition Q214. The value of i is between 0 and N. (This results from the previous postcondition, and from P4).
Postcondition Q215. The body of the loop will be called with values of i between 0 and N-1. (Once i becomes N, it will not be called any more; results from the semantics of the for loop.)
Postcondition Q216. The body of the loop will be called each time with a new value of i, monotonically increasing. (People may forget this, but this is a crucial fact that makes the for loop work.)
Postcondition Q217. The expression vec[i] is well-defined. (This can be proved from Q215 and Q28.)
Postcondition Q218. The statement print(vec[i]) is well-defined.
Postcondition Q219. The expression vec[i] will represent during the iteration all the values from the input vector. (This results from the semantics of the vector, Q216 and Q215; it is similar to Q12.)
Postcondition Q220. The for loop in Listing 2 will print all the values in the given vector.
Phew, we reached the end. We showed that the code in Listing 2 is syntactically correct, is semantically correct, and it performs the intended function (prints all the values in the given vector). This time it took us 20 steps to come to this conclusion, compared to 8 steps needed for Listing 1. Although I was clearly trying to make a point, I tried not to exaggerate the number of postconditions. I tried to follow in my head the actual steps to prove mathematically the functioning of the two code snippets, and then wrote the lemmas that would have appeared.
Subtlety matters
Some readers might argue that we’ve gone to great lengths to prove something that is obvious to most programmers. And there is some truth in that – we’ll cover that a bit later. But, oftentimes, small details can have huge, and potentially disastrous, consequences.
Take a look, for example, at this code:
for (size_t i=vec.size()-1; i>=0; i--) {...}
It looks perfectly normal, but it’s utterly wrong; I can’t count how many times I’ve been bitten by code like this. Or, for the same type of code, forget to subtract 1 from the size of the vector, or to perform a strict comparison with zero. That entirely changes the behaviour of the code.
Also think of cases in which the size of the vector can overflow the capacity of the index type.
There are also variants that do not change the behaviour of the code, and yet they look different enough. One simple example is changing i++ to ++i or i+=1. These changes have a non-zero mental cost when reading the code, which proves that our brain has to do a bit more processing to properly or improperly ‘reason’ about the code.
A new metric for complexity
The whole exercise we undertook with the two loop structures yielded the conclusion that the classical 3-part for loop is more complex than the ranged-for loop. It is more complex in terms of number of steps to reason about it, and it is also more complex considering the number of preconditions we have to use from that point on when reading the code inside the for loop (postconditions turn into preconditions).
But, not only can we say that one is more complex than the other, we can also quantify the difference in complexity. We can obtain this by the following formula:
ReasoningComplexity({P}C{Q}) = |Q|-|P|
In plain English, the reasoning of complexity of the code is the number of post-conditions added by that piece of code that were not present in the initial assumptions (we assume that the assumptions before the code are also kept). Or, informally, reasoning complexity is the number of ideas we have to entertain while trying to mathematically reason about the code.
This metric can give a better indication of the complexity of a code than cyclomatic complexity [McCabe76] or Halstead complexity [Halstead77]. Cyclomatic complexity completely avoids all the code complexities that do not involve branches. In other words, a very complex calculation without branches is equally complex to a simple x=0 assignment. On the other hand, the Halstead complexity measures the complexity purely from a syntactic perspective, without including any semantic elements.
In ideal conditions, the metric we defined above would measure how much effort does a person need to spend to (properly) reason about a particular code.
Pattern matching and limitations for reasoning complexity
The above reasoning complexity has one major flaw: it assumes that programmers properly reason about the code, in the mathematical sense. And, that is far from the truth. I think in this article it’s the first time I’ve tried to reason about a piece of code, and even here, I took many shortcuts.
Instead, programmers do something more like pattern matching on the code. That is, most C++ programmers have seen code similar to the one in Listing 2, and they know what the code does without going over the 20 steps of post-conditions. And, I think that would apply to many programmers who haven’t programmed in C or C++ too, as the ideas about classic for loops are so common in programming.
I like to describe this process in the following way: a person sees a code fragment, and that code fragment starts to resonate with other code that the person has seen before. One can immediately see the similarities and the differences with other code, and one can immediately (but not always logically) draw conclusions. Most of these conclusions can be true, even without making once a proper reasoning.
More generally, a person makes sense of new experiences by resonating with past experiences. And this doesn’t apply only to software. One sees a door, one knows that it may be opened; one sees a chair, and knows that someone might sit on it; one sees an animal like a wolf, one knows that it might do harm.
The fact that our senses are cheating on us is a well-known fact, and yet, every day we rely on our senses to understand what’s happening around us. Pure rationalism doesn’t get us very far (i.e., you can’t be really sure of a single thing), so this type of incomplete reasoning is the only way for us humans to live.
This way of incomplete reasoning we also apply to code, for better or for worse.
A more practical complexity measure
To make our reasoning complexity more practical, we somehow need to incorporate past experience in our formula. Let’s assume that for a given person X, we have a set of Hoare triplets forming the past experience of that person: PE(X)={{Pi}Ci {Qi}}.
With this, the complexity associated for person X to infer conclusions (not mathematical, but rather in a more empirical approach) about a given code is given by:
InferenceComplexity(X,{P}C{Q}) = min(dist({P}C{Q},{P'}C'{Q'}) | {P'}C'{Q'} ∈ PE(X)
with the function dist defined something like:
dist({P}C{Q},{P'}C'{Q'}) = |Q| - |P ∪ Q'|, for C ≈ C'
Now, the above definition is somewhat ambiguous, and that’s almost intentional. Having a non-ambiguous formula here would mean that we thoroughly understand how the brain works, which is far from the truth.
The main idea is that, when trying to define the complexity for a given code, we need to consider also the previous experience of the programmer reading the code. The more the programmer has seen and made inference about that type of code, the simpler the code would be. This is why, for most programmers, the code from Listing 2 is roughly as complex as the code from Listing 1 – we’ve seen that code pattern many times, and we know what it means.
A few takeaways and examples
Now that we have two complexity measures, let’s pick some random examples and see how they can be used for analysing various situations.
There is no one single style to rule them all
What I find to be easy to understand may not be for the next programmer. And vice versa. We constantly have to be aware of our biases.
We can have some general reasoning why certain things might be simpler than other things, but we should always remember that these are context-dependent.
One good example for this is coding styles (read formatting). I’ve seen many passionate arguments from a lot of people, arguing that a certain code style is better than another – some coming from people I respect a lot. But, after a given point, every style choice will be received well by some programmers and painfully by others.
In this category, a good example in the C++ community is the east-const vs west-const debate (I won’t even post a link to it).
My takeaway from this is that I would get familiar with multiple styles of programming, looking at the essential properties of the software, and not at the code style.
Complexity for smaller operations
Apart from the style issues, there are certain practices which seems (to me) very odd. People sometimes add more complexity to the code (in the absolute mode) in the hope of making it simple. This seems a bit counter-intuitive.
Please see Listing 3. In the first if condition, instead of just checking the value of my_bool, we make a new comparison with constant true. This is clearly more complex than just the code if (my_bool), at least for an analytical mind.
bool my_bool = ...; if (my_bool == true) ... int my_int = ...; if (0 == my_int) ... |
| Listing 3 |
The second if clause in Listing 3 is called Yoda conditions [WikiYoda], a reference to Yoda from the Star Wars film, who frequently reverses words. In many languages, people express simple statements in the form ‘subject verb complement’; for example “The grass is green”; we would not typically say “green the grass is”. I think most English-speaking people can understand what “green the grass is” means, but, at the same time, it would be against people’s expectations, and would add extra mental processing (small, but it’s there).
Translating this into software, it tends to be easier for people to read code in the order ‘variable predicate constant’ rather than ‘constant predicate variable’. There were historical reasons for why the Yoda conditions were preferred, but I strongly suggest using the proper tools to solve those problems, and not change the coding style, adding mental effort for most if statements.
But then again, this is a styling issue.
Monads
We can roughly divide the programming world in two: those who know about monads and love them and those who hate monads as they consider them completely abstract. (There is also a joke that most programmers read about monads every couple of months, and then immediately forget about them – but let’s ignore this category.)
For functional programmers, using monads is a day-to-day job, so the inference complexity for reading code with monads is lower than a person who doesn’t use monads frequently.
In reality, monads are simple concepts, and they are heavily used by imperative programmers as well, just that most of the time they don’t pay attention to it. I’ll try a very short pitch to the C++ developers.
A monad is a type wrapper (read template type), plus a type convertor function (called unit or return) that transforms a value into a value of the wrapped type, and another function called combinator (sometimes named bind or flatmap) that transform that monadic type.
The std::optional<T> and std::vector<T> are well known monadic types; the constructors for these types that take T as parameters can be considered the type convertor; functions with the declaration shown in Listing 4 (or similar) can act as combinators.
template <typename T1, typename T2> optional<T2> bind(const optional<T1>& x, function<optional<T2>(T1)> f); template <typename T1, typename T2> vector<T2> bind(const vector<T1>& x, function<vector<T2>(T1)> f); |
| Listing 4 |
The bottom line is that, the reasoning complexity is actually lower than the perceived complexity. So, the inference complexity can also have negative feedback loops. Interesting…
Functional programming vs OOP
After discussing monads, it makes sense to discuss functional programming vs OOP.
It would probably make sense to start an analysis on the reasoning complexity for common structures in the two paradigms, but that’s too far beyond the goal of this article. But, I think it’s safe to say that they probably have the same reasoning complexity.
This means that OOP people have a bias against the complexity coming from functional programming, and functional programming people will have a bias against the complexity coming from OOP programs.
At least for me, with the two metrics of complexity in front of me, I now realise that the major difference between the two paradigms is the perceived complexity. The way to resolve this difference is by learning: people need to get accustomed to the other style of programming.
As linguistics would say, learning a new language means learning a new way to think.
Conclusions
The article tries to analyse what reasoning about code properly means. Formally, we argue that reasoning means deriving the implications of the code. Based on this, we define a new complexity metric, that essentially counts the number of new post-conditions that were added after executing that code.
But this metric doesn’t seem to properly apply in practice. We, as programmers, tend not to reason in the mathematical sense, but rather infer conclusions based on previous experience; we can be occasionally wrong, but it tends to work really well in practice. Thus, we hint at another complexity metric (very informally defined) that considers the experience of the programmer.
Both complexity metrics tend to relate to the effort that the programmer makes (or is assumed to make) when trying to make sense of the code.
This opens the discussion of assessing the complexity of code, from two directions, which are sometimes contradictory. From one perspective, a reasoning complexity tries to have an absolute, independent position for assessing the complexity of the code. This can provide a good basis for discussion, but it often may be impractical. On the other side, the perspective of using inferred complexity tries to look more from the programmer’s point of view, but loses objectivity. This can be used to discuss complexity related to social issues (coding styles, paradigms, etc.).
But, maybe more importantly, as the inferred complexity is learned, we may learn to rely less on it, and use the reasoning complexity. That would provide us better opportunities to reason about reasoning about code.
References
[Halstead77] Maurice H. Halstead. Elements of Software Science. Elsevier North-Holland, 1977
[Henney20] Kevlin Henney, One of the most important observations…, Twitter, https://twitter.com/kevlinhenney/status/1303989725091581952?s=21, 2020
[Hoare69] C. A. R. Hoare, An axiomatic basis for computer programming. Communications of the ACM. 12 (10): 576–580, 1969.
[McCabe76] T. J. McCabe, A Complexity Measure, IEEE Transactions on Software Engineering (4), 1976
[MW] Merriam-Webster, Reason, https://www.merriam-webster.com/dictionary/reason, 2021
[WikiYoda] Wikipedia, Yoda conditions, https://en.wikipedia.org/wiki/Yoda_conditions
[Whitehead10] Alfred North Whitehead; Bertrand Russell, Principia Mathematica, vol 1/2/3 (1 ed.), Cambridge: Cambridge University Press, 1910/1912/1913, https://quod.lib.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=AAT3201.0001.001
has a PhD in programming languages and is a Software Architect at Garmin. He likes challenges; and understanding the essence of things (if there is one) constitutes the biggest challenge of all.











