This article concludes the 3-part series. Cassio Neri presents a new algorithm that also works for 64-bit operands.
The first two instalments of this series [
Neri19
] and [
Neri20
] showed three algorithms,
minverse
,
mshift
and
mcomp
, for evaluating expressions of the form
n % d
⋚
r
, where
d
is known by the compiler and ⋚ denotes any of
==
,
!=
,
<
,
<=
,
>
or
>=
. While
minverse
is restricted to expressions where ⋚ is either
==
or
!=
,
mshift
and
mcomp
are not. However, the last two must perform intermediate calculations in domains larger than their input. Specifically, for 32-bit data, computations are done in 64-bit registers. What if the input is already large? Will we still need it when it is 64? Yes, but these algorithms will not send you a Valentine, birthday greetings or bottle of wine. This article presents another algorithm that overcomes this limitation. I shall refer to it as
new_algo
since, to the best of my knowledge, it is original.
1
All algorithms, including
new_algo
, are implemented in [
qmodular
]. Recall once again that the intention is not to ‘beat’ the compiler but, on the contrary, to help it. The hope is that compiler writers will consider incorporating these algorithms into their products for the benefit of all programmers. As I reported in [
Neri19
],
minverse
has been implemented by GCC since version 9.1 but the implementation falls back to a less efficient algorithm for certain values of
r
. Clang 9.0 also uses
minverse
(only when
r == 0
but its trunk version extends the usage for all other remainders). (See [
Godbolt
].) Other major compilers do not implement
minverse
and none implements any of the other algorithms presented in this series.
Recall and warm up
Figure 1
2
graphs the time taken by different algorithms to check whether each element of an array of 65,536 uniformly distributed unsigned 64-bit dividends in the interval [0, 10
6
] leaves a remainder less than 5 when divided by 7. As usual,
built_in
corresponds to
n % 7 < 5
as emitted by the compiler. (As a motivational note, when
n
is the number of days since a certain Monday,
n % 7 < 5
is a check for weekdays.) Bars labelled
mshift
and
mcomp
correspond to algorithms covered in [
Neri20
]. Finally,
new_algo
is the subject of this article.
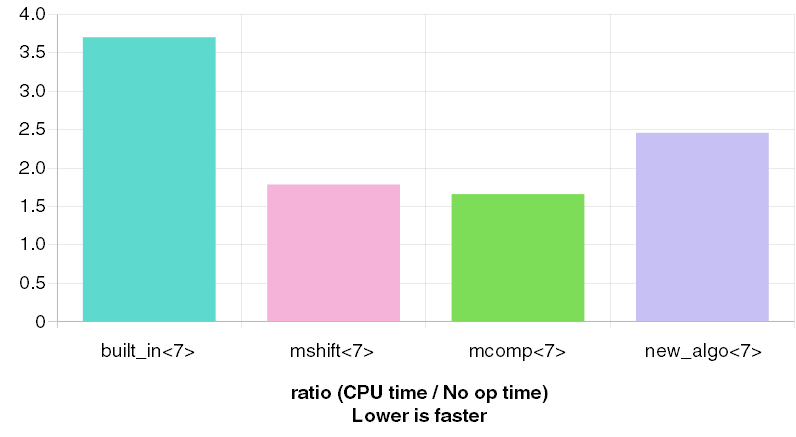
|
| Figure 1 |
Observe that some previously seen algorithms are absent from Figure 1. As explained,
minverse
cannot be used with
<
and efficient implementations of
mshift_promoted
and
mcomp_promoted
for 64-bit inputs require full hardware support for 128-bit calculations, which is not provided by x86_64 CPUs.
Recall that
mshift
and
mcomp
have preconditions and yield wrong results when
n
is above a certain threshold. Therefore, although very fast, the lack of generality forces the compiler to discard them.
The time taken to scan the array of dividends is used as unit of time. All measurements encompass this time. They are
3
3.70 for
built_in
, 1.78 for
mshift
, 1.66 for
mcomp
and 2.46 for
new_algo
. Subtracting the scanning time and taking results relatively to
built_in
’s yields 0.78 / 2.70 ≈ 0.29 for mshift, 0.66 / 2.70 ≈ 0.24 for
mcomp
and 1.46 / 2.70 ≈ 0.54 for
new_algo
. These numbers, however, depend on the divisor. Listing 1 contrasts the code generated by GCC 8.2.1 with
-O3
for
built_in
and
new_algo
.
Finally, recall that we are interested in modular expressions where the divisor is a compile time constant and the dividend is a runtime variable. The value compared to the remainder can be either. They all have the same unsigned integer type which implements modulus 2 w arithmetic . (Typically, w = 32 or w = 64.) We focus on GCC 8.2.1 for the x86_64 target but some ideas might also apply to other platforms.
The new_algo
The fractional part of
n
/
d
corresponds to the remainder of the division. Indeed, Euclidean division states that any integer
n
can be uniquely written as
n
=
q
∙
d
+
r
, where
q
and
r
are integers with 0 ≤
r
<
d
. Dividing this equality by
d
gives that
q
and
r
/
d
are, respectively, the integer and fractional parts of
n
/
d
. Hence, knowing the fractional part of
n
/
d
, or an approximation of it, is enough to identify
r
. Since
The last paragraph’s arguments supported the works of mshift and mcomp [ Neri20 ] and they equally support new_algo . The novelty is that this algorithm, rather than accepting the approximation error until the result becomes unreliable, takes steps to reduce the error. As a consequence, the algorithm’s applicability is extended. As usual in this series, we shall present new_algo ’s main ideas by means of examples. (Deeper mathematical proofs of correctness can be seen in [ qmodular ] and references therein.)
Although a rigorous proof is out of scope, the fundamental idea behind new_algo ’s error reduction has elementary school level 4 : the periodicity of decimal expansions of rational numbers. For example, 1 / 3 = 0.333… and the sequence of 3s goes on indefinitely. Also, 1 / 7 = 0.142857… and 142857 repeats over and over. Some readers might object and point to terminating expansions like 1 / 2 = 0.5 or, even more obvious, 1 / 1 = 1. Nevertheless, a terminating expansion can be identified with a periodic one by appending an infinity of trailing 0s. For instance, 0.5 = 0.5000… and 1 = 1.000…. Furthermore, a terminating expansion is also identified with yet another periodic representation ending in 9s. Indeed, recall (or try to convince yourself) that 0.5 = 0.4999… and 1 = 0.999…. More generally, periodicity occurs for any base and, in particular, in binary expansions. For instance, 1 / 7 = (0.001001...) 2 with repeating 001 bits.
Reality kicks in again to remind us that CPUs have finite precision. In practice
n
,
d
and
r
are 32 or 64 bits long but, for ease of exposition, we assume the number of bits is
w
= 10. Hence, truncation at the 10
th
bit after the binary point yields 1 / 7 ≈ (0.0010010010)
2
. Keeping the example of the previous section in mind, we set
d
= 7 and the approximation
M
= (0.0010010010)
2
of 1 / 7.
Table 1 contrasts, for all n ∈ {0, …, 8}, the binary expansions of n / 7 and n ∙ M . Bits are grouped in triples to highlight the period. Observe that for n ≤ 7, multiplication by 1 / 7 and by M can be done separately on each triple, since the result of one group does not spill to its left. (Take notice that the 2 nd column shows n / 7 = (0.111111…) 2 which is the binary analogon of 1 = 0.999…. This exemplifies the relevance for new_algo of the periodic representation of terminating expansions.)
|
||||||||||||||||||||||||||||||
| Table 1 |
The row for n = 8 is the first where the fractional parts of n / 7 and n ∙ M , up to the 9 th bit, differ. (The relevant triple of bits is emphasised.) To understand the origin of this difference, we observe that this row can be obtained from the one for n = 1 by multiplication by 8 or, equivalently, by left shift by 3. The 2 nd column illustrates infinite precision and the periodicity ensures that any triple of bits after the binary point has a replica on its right which is also left-shifted. This contrasts to the 3 rd column, where the bits feeding the left shift at the rightmost position are 0s. Having realised that there is an error coming from the right, we shall see how new_algo reduces it.
The previous paragraph pointed out a discrepancy between the fractional parts of n / 7 and n ∙ M for n = 8. Observe now the disparity between the integral parts. It turns out the two divergences compensate each other and by uniting the two parts we can correct the error of division.
Figure 2 illustrates the steps of the process (grey 0-bits are included for clarity) as applied to n = 8: right shift the integer part of n ∙ M by 9 bits and add the result to n ∙ M . Comparing the outcome with 8 / 7 (shown in Table 1) we realise it is much closer than the original value 8 ∙ M is.
|
|
| Figure 2 |
The procedure is very effective in making the fractional parts of the result for n = 8 identical to that for n = 1, that is, (0.001 001 001 0) 2 .
The fact that multiplication by n = 8 is equivalent to left shift by 3 bits makes clear that the quantity on the left of the binary point is the exact amount required to correct the error on the right. For other values of n , this property might be more difficult to see but it still holds. For instance, consider n = 15, which is the next dividend with remainder 1. Then n ∙ M = (10. 001 000 111 0) 2 and the correction process in shown in Figure 3. Again, the result’s fractional part matches the one obtained for n = 8. Therefore, the outcomes of the correction for n = 1, n = 8 and n = 15 have all the same fractional part.
|
|
| Figure 3 |
Unfortunately, the process is not so good for all n . Indeed, for n = 519 we have n ∙ M = (1 001 001. 111 111 111 0) 2 and Figure 4 shows that the fractional part of the outcome is off by deficiency when compared to the one obtained for n = 1. The disparity appears at the 9 th bit (emphasised) and thus, the error is still small. By proximity, the result suggests that the remainder is 1, which is correct.
|
|
| Figure 4 |
It is worth noticing that n = 519 is not the smallest value for which the correction attempt does not zero the error out. Indeed, the row for n = 7 of Table 1 shows that the integer part of n ∙ M is 0 and thus, the correction attempt does not provoke any change to the fractional part of n ∙ M = (0. 111 111 111 0) 2 . Moreover, the outcome is quite far from the one for n = 0. This sounds like a showstopper, given that proximity is the key to recognise remainders and it has failed to hold here. Fortunately, this is more an annoyance than a real issue.
Important points to retain follow. As n takes increasing values with the same remainder r > 0, the fractional part of the outcome f ( n ) starts, for n = r , at f ( r ) = r ∙ M and, at each stage, it either stays the same or decreases by a tiny amount. As long as f ( n ) does not fall enough to reach f ( r - 1), we are sure the remainder is r . Furthermore, when r is large enough, f ( n ) does not change at all, that is, f ( n ) = r ∙ M for all n with remainder r in the range of interest.
Therefore, for n in a certain range, the remainder of n divided by d is r if, and only if, ( r - 1) ∙ M < f ( n ) ≤ r ∙ M or, equivalently, r ∙ M < f ( n ) + M ≤ ( r + 1) ∙ M . The analysis of the case r = 0 is a bit trickier but the same result holds. It also follows that the remainder of n divided by d is less than r if, and only if, 0 < f ( n ) + M ≤ r ∙ M .
To finish this section, a very important limitation of new_algo must be mentioned: it is not available for all divisors. Indeed, it is easy to see that, for the correction to work, at least one full period must fit in 10 bits but, as it turns out, the period of 1 / 13 in binary has length 12. Therefore, new_algo cannot be used for d = 13 in our idealised CPU. In a real 64-bit machine the smallest divisor with this issue is d = 67. (The period of 1 / 67 has length 66.)
Towards an implementation
The presentation so far has evolved around the idea of splitting numbers into their integer and fractional parts. We shall see now how to turn this idea into a working implementation based on unsigned integers values only. Again, for ease of exposition, we assume that these numbers and CPU registers are 10-bits long.
The algorithm’s first step is calculating n ∙ M where n is an integer and M has 10 bits after the binary point. To bring the product to the realm of integers, the multiplicand M is substituted by M ∙ 2 10 . To keep the notation simple, the latter quantity is still denoted M . Hence, in our example we set M = (0010010010) 2 .
Another practical issue remains. Now
n
and
M
are 10 bits long and thus, the product
n
∙
M
has up to 20 bits. How can a 10-bit CPU calculate such number? In the real world, the question is how can a x86_64 CPU compute the 128-bit product of two 64-bit operands? The
mul
instruction (see Listing 1) does exactly that, by splitting the 128-bit product into its 64-bit higher and lower parts and storing them in registers
rdx
and
rax
, respectively. Coming back to our exposition, we assume that our imaginary 10-bit CPU provides a similar
mul
instruction.
built_in 0: movabs $0x2492492492492493,%rdx a: mov %rdi,%rax d: mul %rdx 10: mov %rdi,%rax 13: sub %rdx,%rax 16: shr %rax 19: add %rax,%rdx 1c: shr $0x2,%rdx 20: lea 0x0(,%rdx,8),%rax 28: sub %rdx,%rax 2b: sub %rax,%rdi 2e: cmp $0x4,%rdi 32: setbe %al 35: retq new_algo 0: movabs $0x2492492492492492,%rcx a: mov %rdi,%rax d: mul %rcx 10: add %rcx,%rax 13: lea (%rax,%rdx,2),%rdx 17: movabs $0xb6db6db6db6db6da,%rax 21: cmp %rax,%rdx 24: setbe %al 27: retq |
| Listing 1 |
Notwithstanding the change in the definition of M , figures 2, 3 and 4, still illustrate the correction with little differences. Previously, the small dot symbolised the binary point but now it separates the higher and lower parts. To correctly align the bits of the higher part to those of the lower one, the former should be left shifted by k = 1. Finally, we were originally interested in the fractional part of the outcome but now it is the lower part that we care about. In particular, the addition does not need to be carried over to the higher part, it can be performed in modulus 2 10 arithmetic.
Putting all pieces together, a C++ implementation of
new_algo
to evaluate
n % d < r
looks like this:
bool has_remainder_less(uint_t n, uint_t r) {
auto [high, low] = mul(M, n);
uint_t f = low + (high << k);
return f + M <= r * M;
}
where
mul(M, n)
returns a pair of
uint_t
with the higher and lower parts of
M * n
. The last line is the condition 0 <
f
(
n
) +
M
≤
r
∙
M
in simplified form since it can be shown that 0 <
f
(
n
) always holds.
For readers accustomed to x86_64 assembly, it should not be difficult to recognise the C++ code above in Listing 1. (With compile time constants
M = 0x2492492492492492
,
k = 1
and
r * M = 5 * M = 0xb6db6db6db6db6da
).
A naïve implementation of
new_algo
for
n % d == r
follows:
bool has_remainder(uint_t n, uint_t r) {
auto [high, low] = mul(M, n);
uint_t f = low + (high << k);
uint_t fpM = f + M;
return r * M < fpM && fpM <= (r + 1) * M;
}
The last line comes from
r
∙
M
<
f
(
n
) +
M
≤ (
r
+ 1) ∙
M
. This code contains many inefficiencies (e.g., the branch implied by
&&
) and is shown for exposition only. A faster implementation is provided in [
qmodular
]. Depending on a number of factors, many optimisations are possible. For instance, for small values of
k
, the addition and left shift in the second line can be combined in a single
lea
instruction. (See Listing 1.) Also, as we have seen, for larger values of
r
the only condition to be tested is
f
(
n
) =
r
∙
M
. The important point here is that
new_algo
’s final form depends on several aspects that have a visible impact on the performance, as we shall see in the next section.
Performance analysis
As in the warm up, all measurements shown in this section concern the evaluation of modular expressions for 65,536 uniformly distributed unsigned 64-bit dividends in the interval [0, 10 6 ]. Charts show divisors on the x -axis and time measurements, in nanoseconds, on the y -axis. Timings are adjusted to account for the time of array scanning.
For clarity, we restrict divisors to [1, 50] which suffices to spot trends. (Results for divisors up to 1,000 are available in [ qmodular ].) In addition, we filter out divisors that are powers of two since the bitwise trick (see [ Warren13 ]) is undoubtedly the best algorithm for them. The timings were obtained with the help of Google Benchmark [ Google ] running on an AMD Ryzen 7 1800X Eight-Core Processor @ 3600Mhz; caches: L1 Data 32K (x8), L1 Instruction 64K (x8), L2 Unified 512K (x8), L3 Unified 8192K (x2).
Figure 5 concerns the evaluation of
n % d == 0
. Readers might already be familiar with
minverse
’s zigzag and its great performance. Although
mcomp
and
mshift
are even faster and have a pretty regular performance across divisors (a good feature on its own), recall they are not available for all values of
n
. They are shown here for the sake of completeness but in practice a compiler cannot use them. Looking at
new_algo
, we observe that its performance changes considerably across divisors depending on the availability of different micro-optimisations. Actually,
new_algo
is not very performant here and given the limitations of
mcomp
and
mshift
, we conclude that
minverse
is the best option.
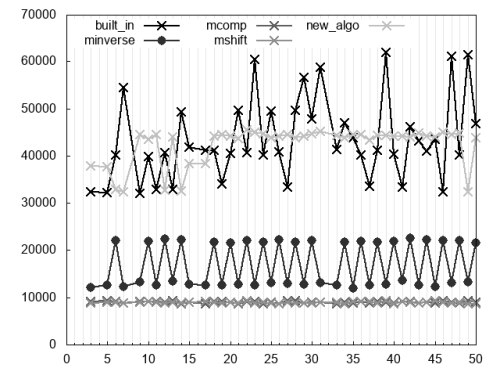
|
| Figure 5 |
Figure 6 shows the evaluation of
n % d == 1
. Due to
mshift
’s and
mcomp
’s limitation, they have now been excluded from this picture. The situation changed considerably with respect to the previous case. Indeed,
new_algo
beats the
built_in
algorithm for all divisors shown and for a handful of them (e.g.,
d
= 14) it even beats
minverse
.
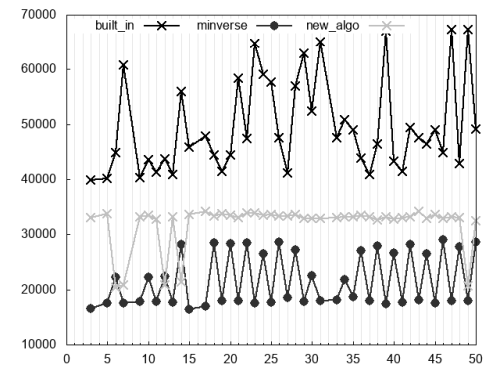
|
| Figure 6 |
Finally, Figure 7 considers the expression
n % d > 1
. Recall that
minverse
cannot evaluate this expression. It is fair to say that
new_algo
beats the
built_in
algorithm for most of the divisors shown in the picture.
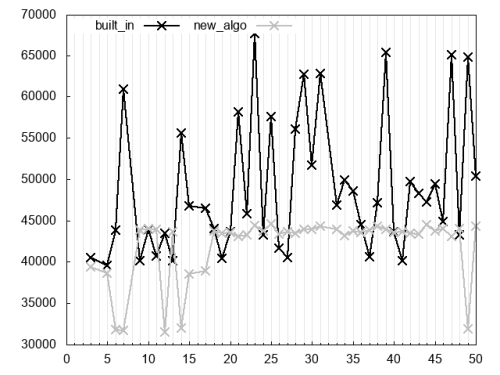
|
| Figure 7 |
Conclusion
We presented a new algorithm, designated here as
new_algo
, for the evaluation of certain modular expressions. It overcomes limitations of other algorithms previously seen in this series [
Neri19
] and [
Neri20
]. Specifically,
minverse
cannot be used for expressions like
n % d < r
and
mshift
and
mcomp
cannot be efficiently implemented in 64-bit CPUs. Alas, the
new_algo
has its own limitation: it is not available for all divisors.
Like mshift and mcomp , new_algo operates on an approximation of n / d. which contains an error that increases with the numerator. Contrarily to the others, new_algo performs steps to delay the error growth by using the periodicity of binary expansions of rational numbers. In essence, errors on the right side of the truncated expansion can be corrected using bits appearing on the left.
Performance analysis shows that, in some cases,
new_algo
can be faster than others. However, it is worth mentioning that no algorithm seen in this series beats all others in all circumstances. Therefore, a compiler aiming to emit the most efficient code for modular expressions needs to implement all these algorithms and carefully pick the one that is best for the particular case in hand. Amongst other aspects, this decision must consider the value of the divisor, the type of the expression (e.g.,
n % d == r
as opposed to
n % d > r
), the size of operands (32 versus 64 bits). A particularly interesting point about
new_algo
is that to emit efficient code just for this one algorithm, the compiler (writer) has already to deal with many choices of micro-optimisations.
This article brings this series to an end but more research is needed. To compiler writers: “I don’t know why you say goodbye, I say hello.”
Acknowledgements
I am deeply thankful to Fabio Fernandes for the incredible advice he provided during the research phase of this project. I am equally grateful to Lorenz Schneider and the Overload team for helping improve the manuscript.
References
[Godbolt] https://godbolt.org/z/xsMLeP
[Google] https://github.com/google/benchmark
[Neri19] Cassio Neri, ‘Quick Modular Calculations (Part 1)’, Overload 154, pages 11–15, December 2019. https://accu.org/index.php/journals/2722
[Neri20] Cassio Neri, ‘Quick Modular Calculations (Part 2)’, Overload 155, pages 14–17, January 2020. https://accu.org/index.php/journals/2748
[QuickBench] http://quick-bench.com/ oF3Bm1mHz3_pbSuLHV4NdqY1edw
[qmodular] https://github.com/cassioneri/qmodular
[Warren13] Henry S. Warren, Jr., Hacker’s Delight , Second Edition, Addison Wesley, 2013.
Footnotes
- I would be grateful if a well-informed reader could point me towards a previous work on the same algorithm.
- Powered by quick-bench.com. For readers who are C++ programmers and do not know this site, I strongly recommend checking it out. In addition, I politely ask all readers to consider contributing to the site to keep it running. (Disclaimer: apart from being a regular user and donor, I have no other affiliation with this site.)
- YMMV, reported numbers were obtained by a single run in quick-bench.com using GCC 8.2 with -O3 and -std=c++17 [ QuickBench ]. I do not know details about the platform it runs on, especially, the processor.
- I cannot help myself from highlighting the beauty of this simplicity.
has a PhD in Applied Mathematics from Université de Paris Dauphine. He worked as a lecturer in Mathematics before moving to the financial industry.











