Concepts can play a role in function overloading. Andrew Sutton shows us how.
This is the third, and long overdue, article in my series on C++ concepts. The first two articles focused on how concepts are used to constrain generic algorithms [ Sutton15 ] and how concepts are defined [ Sutton16 ]. This article describes a sometimes overlooked, frequently misunderstood, and yet extraordinarily powerful feature of concepts: their role in function overloading. Concepts are useful for more than just improving error messages and precise specification of interfaces. They also increase expressiveness. Concepts can be used to shorten code, make it more generic, and increase performance.
Before diving in, it’s worth noting a few things that have happened since the publication of my last article. First, concepts were not included in C++17. Some committee members felt that there hasn’t been sufficient time since the publication of the TS [ N4549 ] to be confident that the design is appropriate, and many were undecided.
Second, GCC 6.2 was released in late August. This version includes a major update to two components of the concepts implementation. The diagnostics generator has been significantly revamped to provide precise diagnostics about the failure of a concept to be satisfied. The support for overloading on constraints (the topic discussed in this article), was completely rewritten to provide dramatic performance gains. In GCC, concepts can now be used for projects of significant size and complexity.
Finally, since concepts was not accepted into C++17, I have seen an increase in online content promoting concept emulation techniques over language support and even claims that expression SFINAE, constexpr if,
static_assert
, and clever metaprogramming techniques are sufficient for our needs. That’s analogous to claiming that given
if
and
goto
, we don’t need
while
,
for
, and range-
for
. Yes, it’s logically correct, but in both cases we drag down the level of abstraction to specifying how things are to be done, rather than what should be done. The result is more work for the programmer, more bugs, and fewer optimization opportunities. C++ is not meant to be just an assembly language for template metaprogramming. Concepts allows us to raise the level of programming and simplify the code, without adding run-time overhead.
Recap
In my previous articles [
Sutton15
,
Sutton16
], I discussed a simple generic algorithm,
in()
, which determines whether an element can be found in a range of iterators. Here is an alternative version of the
in()
algorithm from the previous article. I’ve modified its constraints for the purpose of this article and also updated it to match some current naming trends in the C++ Standard Library (see Listing 1).
template<Sequence S, Equality_comparable T>
requires Same_as<T, value_type_t<S>>
bool in(const S& seq, const T& value) {
for (const auto& x : range)
if (x == value)
return true;
return false;
}
|
| Listing 1 |
This rendition of
in()
takes a sequence instead of a range as its first argument, and an equality comparable value for its second. The algorithm has three constraints:
-
the type of the
seqmust be aSequence, -
the type of
valuemust beEquality_comparable, and -
the
valuetype must be the same as the element type ofseq.
Here,
value_type_t
is a type alias that refers to the declared or deduced value type of
R
. The definitions of the
Sequence
and
Range
concepts needed for this algorithm look like Listing 2.
template<typename R>
concept bool Range() {
return requires (R range) {
typename value_type_t<R>;
typename iterator_t<R>;
{ begin(range) } -> iterator_t<R>;
{ end(range) } -> iterator_t<R>;
requires Input_iterator<iterator_t<R>>();
requires Same_as<value_type_t<R>,
value_type_t<iterator_t<R>>>();
};
}
template<typename S>
concept bool Sequence() {
return Range<R>() && requires (S seq) {
{ seq.front() } -> const value_type<S>&;
{ seq.back() } -> const value_type<S>&;
};
}
|
| Listing 2 |
This specification requires all
Range
s to have:
-
two associated types named by
value_type_tanditerator_t -
two valid operations
begin()andend()that return input iterators, - and that the value type of the range match that of the iterator.
Most
Sequence
s have the operations
front()
and
back()
, which return the first and last elements of the range. This isn’t a fully developed specification of a sequence, but it is sufficient for the discussion in this paper.
This seems reasonable. We can use the algorithm to determine if an element is contained within any sequence. Unfortunately, it no longer works for some collections:
std::set<int> answers { ... };
if (in(answers, 42)) // error: no front()
// or back()
...
This is unfortunate. We should clearly be able to determine if a key is contained within a set. But how do we do this?
Extending algorithms
For someone who knows concepts and the standard library, the solution in this case is obvious: just add another overload that accepts associative containers.
template<Associative_container A,
Same_as<key_type_t<T>> T>
bool in(const A& assoc, const T& value) {
return assoc.find(value) != s.end();
}
This version of
in()
has only two constraints:
A
must be an
Associative_container
, and
T
must be the same as key type of
A
(
key_type_t<A>
). For associative containers, we simply look up
value
using
find()
and then see if we found it by comparing to
end()
. That’s likely to be much faster than a sequential search.
Note that, unlike the
Sequence
version,
T
is not required to be equality comparable. This is because the precise requirements of
T
are determined by the associative container, and those requirements are usually determined by a separate comparator or hash function.
The concept
Associative_container
is defined like Listing 3.
template<typename S>
concept bool Associative_container() {
return Regular<S> && Range<S>() &&
requires {
typename key_type_t<S>;
requires Object_type<key_type_t<S>>;
} &&
requires (S s, key_type_t<S> k) {
{ s.empty() } -> bool;
{ s.size() } -> int;
{ s.find(k) } -> iterator_t<S>;
{ s.count(k) } -> int;
};
}
|
| Listing 3 |
That is, an associative container is
Regular
, defines a
Range
of elements, has a
key_type
(which may differ from the
value_type
), and a set of operations including
find()
, etc.
As with
Sequence
before, this is clearly not an exhaustive list of requirements for an associative container. It doesn’t address insertion and removal, and excludes specific requirements for
const
iterators. Moreover, we haven’t really described how we expect
size()
,
empty()
,
find()
and
count()
to behave. For now, we’ll just rely on our existing knowledge of the Standard Library.
This concept includes all of the associative containers in the C++ Standard Library (
set
,
map
,
unordered_multiset
, etc.). It also includes non-standard-library associative containers, assuming that they expose this interface. For example, this overload would work for all of Qt’s associative containers (
QSet<T>
,
QHash<T>
, etc.) [
Qt
].
To use concepts to extend algorithms, we need to understand how the compiler can tell a plain
Sequence
from an
Associative_container
. In other words, what happens when we call
in()
?
std::vector<int> v { ... };
std::set<int> s { ... };
if (in(v, 42)) // Calls the `Sequence` overload
std::cout << "found the answer...";
if (in(s, 42)) // Calls the
// `Associative_container` overload
std::cout << "found the answer...";
For each call to
in()
, the compiler determines which function is called based on the arguments given. This is called
overload resolution
. This is an algorithm that attempts to find a single best function (amongst one or more candidates) to call based on the arguments given.
Both calls of
in()
refer to templates so the compiler performs template argument deduction and then form function declaration specializations based on the results. In both cases, deduction and substitution succeed in the usual and predictable way, so we have to choose amongst two specializations at each call site. This is where the constraints enter into the equation. Only functions whose constraints are satisfied can be selected by overload resolution.
In order to determine if a function’s constraints are satisfied, we substitute the deduced template arguments into the associated constraints of the function’s template declaration, and then we evaluate the resulting expression. The constraints are satisfied when substitution succeeds, and the expression evaluates to
true
.
In the first call to
in()
, the deduced template arguments are
std::vector<int>
and
int
. These arguments satisfy the constraints of
Sequence
but not those of the
Associative_container
because a
std::vector
does not have
find()
or
count()
. Therefore, the
Associative_container
candidate is rejected, leaving only the
Sequence
candidate.
In the second call to
in()
, the deduced arguments are
std::set<int>
and
int
. The resolution is the opposite of the one before: a
std::set
is never a
Sequence
because it lacks
front()
and
back()
, so that candidate is rejected, and overload resolution selects the
Associative_container
candidate.
In this cases the resolution is straightforward, and many readers will readily recognize the similarity to the
enable_if
technique used today. This works because the constraints on both overloads are sufficiently exclusive to ensure that a container satisfies the constraints of one template or the other, but not both.
The situation gets a bit more interesting if we want to add more overloads of this algorithm. We could extend the algorithm for specific types or templates like we might have done without concepts. Essentially, we could enumerate the valid definitions of
in()
for those types. For example, extending
in()
for WinRT’s
Map
class [
WinRT
] might require a declaration like this:
template<typename K, typename V, typename C>
bool in(const Platform::Collections
::Map<K, V, C>& map, const K& k) {
return map.HasKey(k);
}
When there are many such viable definitions, this quickly becomes tedious and unmanageable. For any data structure that might represent a set of keys, we need a new overload. This simply does not scale.
If we’re lucky, many of those new enumerated overloads will have identical definitions. That would certainly be the case for WinRT’s
Map
and
MapView
classes; both would return
map.HasKey(k)
. In that case, we can unify their definitions into a single, more general template with appropriate constraints. For example:
template<WinRtMap M>
bool in(const M& map, const key_type_t<M>& k) {
return map.HasKey(k);
}
Here,
WinRtMap
would be a concept requiring members common to both
Map
and
MapView
. This would also accept any other map implementations that the library accrues over time, assuming they satisfied the
WinRtMap
constraints.
In general, we can continue extending the definition of a generic algorithm by adding overloads that differ only in their constraints. There are exactly three cases that we need to consider when overloading with concepts:
- Extend a definition by providing an overload that works for a completely different set of types. The constraints of these new overloads would either be mutually exclusive or have some minimal amount of overlap with existing constraints.
- Provide an optimized version of an existing overload by specializing it for a subset of its arguments. This entails creating a new overload that has stronger constraints than it’s more general form.
- Provide a generalized version that is defined in terms of constraints shared by one or more existing overloads.
The three cases can easily be thought of in terms of the Venn Diagrams shown in Figure 1, which shows the possible relationships between the constraints of overloaded functions.
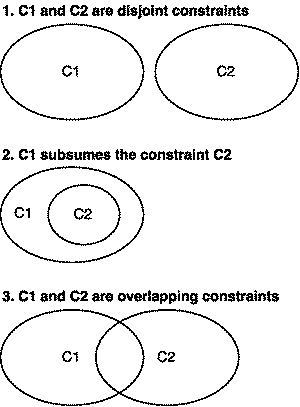
|
| Figure 1 |
Each case in the Figure 1 corresponds to one of the cases above. This section is primarily an example the first case because we generally expect
Sequence
s and
Associative_container
s to be fundamentally different data abstractions.
When constraints are not (mostly) disjoint multiple candidates can be viable, the compiler must determine the best possible candidate for the call. I explain this process in the next section. However, if the compiler can’t determine a best candidate, the resolution is ambiguous. In fact, this is the reason I changed the first
in()
algorithm to require
Sequence
s instead of just
Range
s. It minimizes the amount of overlap and therefore likelihood of ambiguity.
Having disjoint constraints does not guarantee that a call will be unambiguous. We could, for example, try to define a container that satisfies the requirements of both
Sequence
and
Associative_container
. In this case, both overloads would be viable, but neither overload is inherently better than the other. Unless we added new overloads to accommodate this kind of data structure, the result would be an ambiguous resolution.
That said,
Sequence
and
Associative_container
actually do have overlapping constraints; they both require the
Range
concept. We could consider these overloads as being an instance of the third case. This hints that there may be an algorithm that can be defined in terms of the intersecting requirements. But it’s not quite so simple. I intend to discuss these issues in a future article.
The second case is an important feature of generic programming in C++ and is the basis of type-based optimizations in generic libraries. Constraint subsumption allows us to optimize generic algorithms based on the interfaces provided by their arguments. This is the topic of the next section.
Specializing algorithms
For this section, we will leave behind our familiar
in()
algorithm and focus on the C++ iterator hierarchy because it naturally lends itself to this discussion.
In some cases, we can define data structures with an extended set of properties or operations that can be used to define more permissive or more efficient versions of an algorithm. This idea is are embodied by the standard library’s iterator hierarchy of iterators.
Forward iterators can be used to traverse a sequence in only one direction (forward) by advancing one element at a time using
++
. Listing 4 is a simple concept for forward iterators.
template<typename I>
concept bool Forward_iterator() {
return Regular<I>() && requires (I i) {
typename value_type_t<I>;
{ *i } -> const value_type_t<I>&;
{ ++i } -> I&;
};
}
|
| Listing 4 |
Based on this concept, we can define two useful algorithms: one that advances multiple steps using a loop and one that computes the number of steps between two iterators (see Listing 5).
template<Forward_iterator I>
void advance(I& iter, int n) {
// precondition: n >= 0
while (n != 0) { ++iter; --n; }
}
template<Forward_iterator I>
int distance(I first, I limit) {
// precondition: limit is reachable from first
for (int n = 0; first != limit; ++first, ++n)
;
return n;
}
|
| Listing 5 |
For
advance()
,
n
must be non-negative because forward iterators cannot go backwards. Bidirectional iterators, however, can be used to traverse a sequence in both directions (forward and backward) by advancing one element at a time using
++
or
--
. Here is that concept.
template<typename I>
concept bool Bidirectional_iterator() {
return Forward_iterator<I>() && requires (I i)
{
{ --i } -> I&;
};
}
Bidirectional_iterator
is defined in terms of
Forward_iterator
. In other words, a bidirectional iterator is a forward iterator that can also move backwards.
Bidirectional_iterator
’s set of requirements completely subsumes that of
Forward_iterator
(case 2 in Figure 1). As a result, whenever
Bidirectional_iterator<X>
is true (for all
X
),
Forward_iterator<X>
must also be true. In this case we say that
Bidirectional_iterator
refines
Forward_iterator
.
This refinement lets us define a new version of
advance()
that can move in both directions.
template<Bidirectional_iterator I>
void advance(I& iter, int n) {
if (n > 0)
while (n != 0) { ++iter; --n; }
else if (n < 0)
while (n != 0) { --iter; ++n; }
}
The
Bidirectional_iterator
concept allows us to relax the precondition of
advance()
, so that we can used negative values of
n
. On the other hand,
Bidirectional_iterator
provides no new information that could help us improve
distance()
.
We can, however, provide optimizations of both
advance()
and
distance()
for random access iterators. These iterators can be used to traverse a sequence in two directions but can advance multiple elements in one ‘step’ using
+=
or
-=
. We can also count the distance between two iterators by subtracting them. A simplified version of that concept can be defined like this:
template<typename I>
concept bool Random_access_iterator() {
return Bidirectional_iterator<I>() &&
requires (I i, int n) {
{ i += n } -> I&;
{ i -= n } -> I&;
{ i - i } -> int;
};
}
The
Random_access_iterator
concept refines
Bidirectional_iterator
; it adds three new required operations. By providing these operations, we can construct a optimized versions of
advance()
and
distance()
that do not require loops.
template<Random_access_iterator I>
void advance(I& iter, int n) {
iter += n;
}
template<Random_access_iterator I>
int distance(I first, I limit) {
return limit - first;
}
We can use these algorithms to define a large number of useful operations. For example, Listing 6 is an implementation of
binary_search
.
template<Forward_iterator I, Ordered T>
requires Same_as<T, value_type_t<I>>()
bool binary_search(I first, I limit,
T const& value) {
if (first == limit)
return false;
auto mid = first;
advance(mid, distance(first, limit) / 2);
if (value < *mid)
return search(first, mid, value);
else if (*mid < value)
return search(++mid, limit, value);
else
return true;
}
|
| Listing 6 |
The algorithm is defined for forward iterators, but of course it can also be used for bidirectional and random access iterators too. The versions of
advance()
and
distance()
that are used depend on the kind of iterator passed to the algorithm. When used with forward and bidirectional iterators, the algorithm is linear in the size of the input range. For random access iterators, the algorithm is much faster since
distance()
and
advance()
don’t require extra traversals of the input sequence.
The ability to specialize algorithms by constraints and by types is critical for the performance of C++ generic libraries. Simply put, this is the killer app of templates and generic programming. Concepts make it much easier to define and use these specializations. But how does the compiler know which overload to choose?
In the previous examples using sequences and associative containers, only one overload of
in()
was ever viable since the arguments were either one or the other, but not both. However, if we call
binary_search()
with random access iterators, say pointers into an array, all three overloads of
advance()
and both overloads of
distance()
will be viable. This makes sense. Every implementation of those functions are perfectly well defined for pointers.
In this case, the compiler must choose the best amongst the viable candidates. Roughly speaking, C++ considers one function to be ‘better’ than another using the following rules:
- Functions requiring fewer or ‘cheaper’ conversions of the arguments are better than those requiring more or costlier conversions.
- Non-template functions are better than function template specializations.
-
One function template specialization is better than another its parameter types are more specialized. For example,
T*is more specialized thanT, and so isvector<T>, butT*is not more specialized thanvector<T>, nor is the opposite true.
The Concepts TS adds one more rule:
- If two functions cannot be ranked because they have equivalent conversions or are function template specializations with equivalent parameter types, then the better one is more constrained . Also, unconstrained functions are the least constrained.
In other words constraints act as a tie-breaker for the usual overloading rules in C++. The ordering of constraints (more constrained) is essentially determined by the comparing sets of requirements for each template to determine if one is a strict superset of another.
In order to compare constraints, the compiler first analyzes the associated constraints of the function in order to build a set of so-called atomic constraints. They are ‘atomic’ because they cannot be broken down into smaller bits. Atomic constraints includes C++ constant expressions (e.g., type traits) and requirements in a requires-expression .
For example, in the resolution of
advance()
, when called with a random access iterator, the set of constraints for each overload are:
| Concept | Atomic requirements |
|---|---|
Forward_iterator |
value_type_t<I>
{ *i } -> value_type_t<I> const&
{ ++i } -> I&
|
Bidirectional_iterator |
value_type_t<I>
{ *i } -> value_type_t<I> const&
{ ++i } -> I&
{ --i } -> I&
|
Random_access_iterator |
value_type_t<I>
{ *i } -> value_type_t<I> const&
{ ++i } -> I&
{ --i } -> I&
{ i += n } -> I&
{ i -= n } -> I&
{ i - j } -> int
|
For brevity, I excluded the
Regular<I>
constraint appearing in
Forward_iterator
since it (and its requirements) are common to all iterator concepts. Comparing these, we find that
Bidirectional_iterator
has a strict superset of the requirements of
Forward_iterator
, and
Random_access_iterator
has a strict superset of the requirements of
Bidirectional_iterator
. Therefore,
Random_access_iterator
is the most constrained, and that overload is selected.
The new overloading rule does not guarantee that overload resolution will succeed. In particular if the two viable candidates have overlapping or logically equivalent constraints, the resolution will be ambiguous. There are a few of reasons this might happen.
Semantic refinement
In some cases, refinements are purely semantic. They do not not provide operations that the compiler can use to differentiate overloads. In fact, this problem appears in the standard iterator hierarchy: input and forward iterators share exactly the same set of operations.
Conceptually an input iterator is an iterator that represents a position in an input stream. As an input iterator is incremented, previous elements are consumed. That is, previously accessed elements are no longer reachable through that iterator or any copy of that iterator. In contrast, forward iterator do not consume their elements when incremented. Previously accessed elements can be accessed by copies. This is typically referred to as the multipass property. This is a purely semantic property. Listing 7 is a concept for input iterators and an revised concept for forward iterators.
template<typename I>
concept bool Input_iterator() {
return Regular<I>() && requires (I i) {
typename value_type_t<I>;
{ *i } -> value_type_t<I> const&;
{ ++i } -> I&;
};
}
template<typename I>
concept bool Forward_iterator() {
return Input_iterator<I>();
}
|
| Listing 7 |
All of the syntactic requirements are defined in the
Input_iterator
concept. The
Forward_iterator
concept just includes
Input_iterator
s. In other words,
Forward_iterator
’s set of requirements is exactly the same as that of
Input_iterator
’s. If we tried to define overloads requiring these concepts, the result would always be ambiguous (neither is better than the other).
Differentiating between these concepts is actually useful. For example, one of
vector
’s constructors (see Listing 8) has a more efficient implementation for forward iterators than for input iterators.
template<Object_type T, Allocator_of<T> A>
class vector {
template<Input_iterator I>
requires Same_as<T, value_type_t<I>>()
vector(I first, I limit) {
for ( ; first != limit; ++first)
push_back(*first); // O(log n) allocations
}
template<Forward_iterator I>
requires Same_as<T, value_type_t<I>>()
vector::vector(I first, I limit) {
reserve(distance(first, limit));
// 1 allocation
insert(begin(), first, limit);
}
// ...
|
| Listing 8 |
This doesn’t work if the compiler can’t tell a
Forward_iterator
from an
Input_iterator
.
We can fix this by adding new syntactic requirements to the
Forward_iterator
concept that relate to its rank in the iterator hierarchy. This has traditionally been done using
tag dispatch
: associating a tag class (an empty class in an inheritance hierarchy) with iterator type for the purpose of selecting appropriate overloads. That associated type is its
iterator_category
. A revised
Forward_iterator
might look like this:
template<typename I>
concept bool Forward_iterator() {
return Input_iterator<I>() && requires {
typename iterator_category_t<I>;
requires Derived_from<I,
forward_iterator_tag>();
};
}
With this definition,
Forward_iterator
’s requirements now subsume those of
Input_iterator
, and the compiler can now differentiate the overloads above. As an added benefit, using random access iterators will be even more efficient since
distance()
requires only a single integer operation.
As another example, C++17 adds a new iterator category: contiguous iterators. A contiguous iterator is a random access iterator whose referenced objects are allocated in adjacent regions of memory whose addresses increase with each increment of the iterator. This opens the door to a number of low-level memory optimizations. It’s also quite obviously a purely semantic property. So if we want to define a new concept, we’ll need to differentiate it from
Random_access_iterator
. Fortunately, we just defined the machinery to do so.
template<typename I>
concept bool Contiguous_iterator() {
return Random_access_iterator<I>() && requires {
requires Derived_from<I,
contiguous_iterator_tag>();
};
}
|
| Listing 9 |
Tag classes are not the only way to solve this problem. I’m just reusing existing standard library infrastructure to solve the problem in this paper. In fact, the only concepts that require these tag classes are
Forward_iterator
and
Contiguous_iterator
. We don’t actually need any of the other tag classes. We could simply use an associated type trait, variable template, or even an extra operation. In other words, we could do something like Listing 10 for forward iterators.
template<typename T>
constexpr bool is_forward_iterator_v = false;
template<typename T>
constexpr bool is_forward_iterator_v<T*> = true;
template<typename I>
concept bool Forward_iterator() {
return Input_iterator<I>() &&
is_forward_iterator_v<T*>;
}
|
| Listing 10 |
All of these approaches would yield the same result; the ability for the compiler to differentiate overloads requiring these concepts.
As a general rule, this technique should only be used to differentiate concepts that vary only in their semantics. Prefer to define concepts so that their interfaces reflect their different semantics.
Conclusions
In this article, we took a first look at how concepts can be used to extend and specialize algorithms through overloading. These ideas have been around for a long time, and in that time, we’ve developed some fairly advanced type-based techniques to manipulate overload outcomes. With concepts, these ideas are codified as part of the language; you simply write appropriate constraints for your algorithms and overload resolution does all the hard work for you.
At least, that’s the ideal. Sometimes it can be a bit tricky to avoid ambiguities when there are overlapping constraints. Case in point, I’ve had to massage the constraints on the
in()
algorithm to make these examples work, but they do work. The next article in this series will be dedicated to the generalization of constrained algorithms and techniques for untangling ambiguous resolutions.
Acknowledgements
Bjarne Stroustrup provided a number of suggestions to improve the structure and content of this article.
References
[N4549] Sutton, Andrew (ed). ISO/IEC Technical Specification 19217. Programming Languages – C++ Extensions for Concepts, Aug 2015.
[Qt] Qt. ‘Qt Documentation: Container Classes’. http://doc.qt.io/qt-4.8/containers.html .
[Sutton15] ‘Introducing concepts’. ACCU Overload . Vol 129. Oct 2015.
[Sutton16] ‘Defining concepts’. ACCU Overload . Vol 131. Oct 2105.
[WinRt] ‘WinRT Documentation: Platforms::Collections::Map Class’. https://msdn.microsoft.com/en-us/library/hh441508.aspx .











