Optimising data processing is often about compromise. Andy Balaam finds the right balance.
The latest release of our product focuses on scalability. We need to enable our users to work with much larger models, and previously they were hitting a hard limit when our 32-bit application went beyond the 2GB address space available on a normally-configured Windows machine.
Of course, there are many ways we can reduce the amount of memory we consume for each element of a model which we hold in memory, but reducing memory usage in this way does not solve the fundamental problem: if we hold it all in memory, there will always be a limit on the size of model we can work with.
In order to be able to handle models of arbitrary size, we needed to find algorithms that work with subsets of the model that are of manageable size. This article describes and compares some of the algorithms we tried in order to make our application scalable.
We began with the non-scalable approach of having everything in memory at once, and set off in the direction of scalability by implementing a naive strategy. This proved to be very slow, so we improved the execution time by making incremental changes to our approach. The algorithm we arrived at achieves bounded memory usage and acceptable performance, without imposing a heavy burden in terms of algorithmic complexity.
The models and algorithms will be illustrated in C++ using the BOOST Graph Library (BGL) [ BGL ]. To test our algorithms we will run them against randomly-generated models.
The model
The models in our application may be thought of as directed graphs - that is, sets of 'nodes' which are connected by 'edges', where each edge has a direction. Cycles (paths between nodes that end up where they started) are allowed.
Figure 1 shows an example of a directed graph. The graph shown may be partitioned into three disconnected sub-graphs, indicated by the ovals. The importance of our ability to partition such graphs in this way will become clear later.
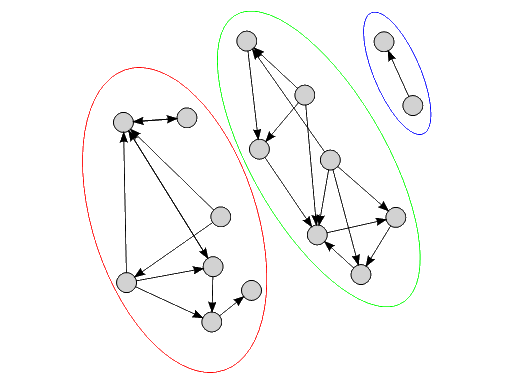
|
| Figure 1 |
The edges indicate dependencies in our model. What this means in practice is that if A depends on B (i.e. the nodes A and B are connected by an edge which is directed from A to B) then it does not make sense for A to be in memory without B. Our algorithms are required to work in a scalable way within this constraint. This, of course, means that certain models (e.g. where chains of dependencies mean that all nodes are required at once) simply cannot be handled in a scalable way. Fortunately, in practice the models we work with are decomposable into smaller graphs despite this constraint 1 .
In order to test the algorithms we will discuss, we implement them using BOOST Graph Library, with the typedefs and using declarations shown in listing 1. Note that BGL prefers the term 'vertex' whereas in this article we use 'node' to indicate graph nodes.
#include <deque>
#include <set>
#include <boost/graph/adjacency_list.hpp>
using namespace std;
using namespace boost;
typedef adjacency_list<vecS, vecS,
bidirectionalS> DependencyGraph;
typedef graph_traits<DependencyGraph>::
vertices_size_type nodes_size_t;
typedef graph_traits<DependencyGraph>::
vertex_descriptor Node;
|
| Listing 1 |
We need many examples of possible models to evaluate our algorithms. The code in listing 2 shows how we generate random graphs. To create a graph (whose nodes are represented simply as integers) we construct a DependencyGraph object and supply the number of nodes required. To add edges we call the BGL function add_edge .
DependencyGraph create_random_graph(
nodes_size_t num_nodes, size_t num_edges )
{
DependencyGraph ret_graph( num_nodes );
for( size_t edge_num = 0; edge_num < num_edges;
++edge_num )
{
add_edge( rand() % num_nodes,
rand() % num_nodes, ret_graph );
}
return ret_graph;
}
|
| Listing 2 |
At the moment, our users are working with graphs of about 700 nodes and 800 edges, so these are the numbers we will use when generating graphs for testing.
For the formal tests, we will ensure the random seed is set to a consistent value at the beginning of each test. This will mean that the various algorithms are compared against an identical set of graphs.
The task
Our application performs a number of different actions. The action with which we are concerned here involves visiting all nodes and edges of the graph at least once.
In order to scale, our algorithm must limit the number of nodes that are loaded into memory at any time. In order to perform well, our algorithm must minimize the number of times each node is loaded (ideally to one) and minimize the number of loading events that happen.
For our application, the number of nodes that may be loaded at one time (before we run out of memory) is approximately 400, so that will be our limit.
The algorithm in place before we began, which we shall call 'all-at-once' performs just one load event (load everything) and (therefore) loads each node only once. So this algorithm represents the best-case scenario in terms of performance 2 but fails to scale because there is no limit on the number of nodes loaded at any time.
To test our algorithms we need to provide a utility class that tracks their behaviour and provides them with information. The interface for this class, IGraphLoader , is shown in listing 3.
class IGraphLoader
{
public:
virtual void LoadNodes(
const set<Node>& nodes ) = 0;
virtual unsigned int GetMaxNodes() const = 0;
};
|
| Listing 3 |
IGraphLoader declares the LoadNodes method, which an algorithm may call to perform a load event. The supplied argument specifies which nodes should be loaded. In our test code, the implementation simply records the fact that the load event that has taken place so that we can provide statistics and check that all nodes have been loaded at least once when the algorithm completes.
It also declares the GetMaxNodes method, which tells an algorithm how many nodes it is allowed to load before it will run out of memory.
The all-at-once algorithm may be expressed in code as shown in listing 4.
namespace
{
set<Node> create_all_nodes_set(
nodes_size_t num_v )
{
set<Node> ret;
for( nodes_size_t i = 0; i != num_v; ++i )
{
ret.insert( Node( i ) );
}
return ret;
}
}
void algorithm_all_at_once(
const DependencyGraph& graph,
IGraphLoader& loader )
{
loader.LoadNodes( create_all_nodes_set(
num_vertices( graph ) ) );
}
|
| Listing 4 |
The result of running this algorithm against 1000 random graphs is:
....
Percentage of failures: 100
Average number of individual node loads: 700
Average number of load events: 1
Average largest load size: 700
Average batch calculation time: 0.001329 seconds
....
The all-at-once algorithm loads each node once, and performs only one load event, but all of its runs fail because they load 700 nodes at a time, even though our maximum limit is 400. What this means is that in reality our application would crash and not be able to complete the action. This is obviously not an acceptable solution.
'Average batch calculation time' means the amount of time spent calculating which nodes to load. In this case it is very small since we do no work at all, and just load everything. This gives us a measure of the complexity of our algorithm, but is likely to be insignificant to the running time of the real program, since actually performing load events takes much longer, and that time is not included in this total.
The naive solution
In our first pass at making our application scalable, we chose a very naive solution to this problem. The solution was simply to load each node and its dependencies one by one, which we shall call 'one-by-one'.
The code for this algorithm is shown in listing 5.
void algorithm_one_by_one(
const DependencyGraph& graph,
IGraphLoader& loader
)
{
DependencyGraph::vertex_iterator vit, vend;
for( tie( vit, vend ) = vertices( graph );
vit != vend; ++vit )
{
set<Node> s;
s.insert( *vit );
loader.LoadNodes( s );
}
}
|
| Listing 5 |
The result of running this algorithm against 1000 graphs is:
....
Percentage of failures: 0
Average number of individual node loads: 30143
Average number of load events: 700
Average largest load size: 223
Average batch calculation time: 0.019482 seconds
....
The one-by-one algorithm has a very low number of failures (in practice in our application, no failures) because it always keeps the number of nodes loaded to an absolute minimum. However, it performs a very large number of load events, and loads a very large number of nodes, since many nodes are loaded multiple times.
In our real application, this algorithm can take 30-40 minutes to complete, which is completely unacceptable for our users.
Because the process takes so long, there is almost no limit to the amount of pre-processing we should do if it improves performance. Even if our pre-processing step took a whole minute (which would imply an extremely complex algorithm) it would be a net gain if it improved performance by as little as 2.5%. However, it is desirable to keep complexity to a minimum to reduce the maintenance burden for this code.
Avoiding unneccesary work
The one-by-one algorithm reduces memory usage to a minimum, but has very poor performance, while the all-at-once algorithm has better performance (if it didn't crash) and far too much memory usage. We should be able to find solutions in the middle ground of the memory usage/performance trade-off.
The first observation to make is that if A depends on B, then B and all its dependents will be loaded when we load A. Thus we can improve on the one-by-one algorithm simply by skipping B - it will be covered when we do A.
In code, we have a helper function get_minimal_set , which finds a set of nodes that cover the whole graph if you include their dependencies. It is shown in listing 6.
void remove_from_set( set<Node>& set_to_modify,
const set<Node>& set_to_remove )
{
set<Node> difference_set;
set_difference( set_to_modify.begin(),
set_to_modify.end(), set_to_remove.begin(),
set_to_remove.end(),
inserter( difference_set,
difference_set.begin() ) );
set_to_modify.swap( difference_set );
}
set<Node> get_minimal_set(
const DependencyGraph& graph )
{
set<Node> minimal_set;
set<Node> covered_set;
DependencyGraph::vertex_iterator vit, vend;
for( tie( vit, vend ) = vertices( graph );
vit != vend; ++vit )
{
// Skip the node if it has been covered
if( covered_set.find(
*vit ) != covered_set.end() )
{
continue;
}
// Find all the dependencies of this node
set<Node> this_node_deps_set;
this_node_deps_set.insert( *vit );
expand_to_dependencies( this_node_deps_set,
graph );
// Remove them all from the minimal set
// (since they are covered by this one)
remove_from_set( minimal_set,
this_node_deps_set );
// Add this node to the minimal set
minimal_set.insert( *vit );
// Add its dependencies to the covered set
covered_set.insert(
this_node_deps_set.begin(),
this_node_deps_set.end() );
}
return minimal_set;
}
|
| Listing 6 |
And once we have that helper, the algorithm itself, which we shall call skip-dependents , is simple. It is shown in listing 7.
void algorithm_skip_dependents( const DependencyGraph& graph, IGraphLoader& loader )
{
set<Node> minimal_set = get_minimal_set(
graph );
// Load each node in the minimal set one by
// one (similar to "one-by-one" algorithm).
for( set<Node>::const_iterator msit =
minimal_set.begin();
msit != minimal_set.end(); ++msit )
{
set<Node> s;
s.insert( *msit );
loader.LoadNodes( s );
}
}
|
| Listing 7 |
The result of running this algorithm against 1000 random graphs is:
....
Percentage of failures: 0
Average number of individual node loads: 9785
Average number of load events: 223.188
Average largest load size: 223
Average batch calculation time: 0.038484 seconds
....
The skip-dependents algorithm is functionally identical to one-by-one - it simply avoids doing unnecessary work. It works much faster than one-by-one, and fails just as infrequently.
However, the performance of skip-dependents is still poor. We can do much better by handling nodes in batches.
Batches of nodes
We need to reduce the number of nodes that are loaded more than once, and reduce the overall number of load events, so we gather our nodes into batches, and process several at once. Each batch with all its dependencies should be smaller than the maximum number of nodes we can fit in memory, but (if we ignore the performance impact of using a large amount of memory) we should load as many nodes as possible within this constraint. A very simple application of this idea is an algorithm we will call 'arbitrary-batches'.
Arbitrary batches
The arbitrary-batches algorithm handles the nodes in an arbitrary order. It starts with the first node and calculates its dependency set. If the set is smaller than the maximum number of nodes, it adds the second node and its dependencies to the set and again compares its size with the maximum. When the number of nodes goes over the maximum, it stops and reverts to the previous set, and loads it. It now continues with the node that was rejected from the previous set and repeats the process until all nodes have been loaded.
To implement this algorithm we will need a small helper function get_dependency_set_size , shown in listing 8.
size_t get_dependency_set_size(
const set<Node>& set_to_examine,
const DependencyGraph& graph )
{
set<Node> set_with_deps = set_to_examine;
expand_to_dependencies( set_with_deps, graph );
return set_with_deps.size();
}
|
| Listing 8 |
The main code for arbitrary-batches is shown in listing 9.
void algorithm_arbitrary_batches(
const DependencyGraph& graph,
IGraphLoader& loader )
{
set<Node> minimal_set = get_minimal_set(
graph );
set<Node> current_set;
set<Node> proposed_set;
// current_set is the set that currently fits
// into our maximum size (or a set of size 1,
// which may not fit, but is as small as we can
// go).
// Loop through all the elements. For each
// element, try to add it to the proposed_set.
// If it doesn't fit, load current_set.
for( set<Node>::const_iterator msit =
minimal_set.begin();
msit != minimal_set.end(); ++msit )
{
proposed_set.insert( *msit );
// If proposed_set contains more than one
// element, and is too big, reject it and
// load current_set.
if( proposed_set.size() > 1 &&
get_dependency_set_size( proposed_set,
graph ) > loader.GetMaxNodes() )
{
loader.LoadNodes( current_set );
// Now reset to form the next batch
proposed_set.clear();
proposed_set.insert( *msit );
current_set.clear();
}
// proposed_set is now acceptable, so make
// current_set identical to it by adding the
// node.
current_set.insert( *msit );
}
if( !current_set.empty() )
{
loader.LoadNodes( current_set );
}
}
|
| Listing 9 |
The result of running this algorithm against 1000 random graphs is:
....
Percentage of failures: 0
Average number of individual node loads: 1500
Average number of load events: 4.065
Average largest load size: 399
Average batch calculation time: 0.051833 seconds
....
This shows a huge improvement over the skip-dependents algorithm. We tend to use almost as much memory as we are allowed, but perform far fewer load events, and load far fewer nodes in total, so the execution time is much smaller.
Optimal batches?
Of course, we can do better than batching nodes in an arbitrary way. In theory we could find the optimum batching arrangement by examining all possible batches of nodes and picking the arrangement that results in the smallest number of batches that are within the maximum size. We will call this algorithm 'examine-all-batches'.
An algorithm for finding all partitions of a set (another way of saying all ways of batching our nodes) may be found in [ Knuth ] ('Algorithm H'), along with a discussion of how many partitions we will find for different sizes of set. Actually implementing this algorithm, however, could be argued to be a waste of time, since the number of possible batching arrangements of 700 nodes is 476 795 136 047 527 242 582 586 913 131 035 910 496 255 527 061 253 540 132 105 027 619 533 786 105 963 583 061 633 341 766 382 837 389 648 611 612 771 677 592 830 522 886 078 735 705 416 705 452 453 008 326 983 118 350 278 856 293 246 415 442 825 525 872 132 767 880 703 611 269 517 916 410 699 389 083 898 617 416 296 436 067 998 980 619 863 172 119 737 049 355 905 570 755 067 439 951 890 427 106 073 603 254 568 375 246 887 867 651 403 802 347 197 578 978 486 150 503 432 889 024 029 158 705 125 174 242 857 617 441 606 128 695 723 264 050 292 389 444 854 049 797 955 371 493 350 209 036 229 336 528 542 064 073 126 866 607 390 273 651 430 141 623 552 713 645 986 307 716 444 010 184 419 181 435 356 236 135 376 448 679 116 971 311 289 633 490 791 588 028 597 283 628 657 999 477 361 757 107 291 731 808 263 591 659 810 246 723 306 278 903 986 141 179 776 725 930 061 451 455 179 970 017 669 748 814 194 612 040 515 465 108 922 158 960 995 325 054 798 370 278 578 711 015 636 790 696 712 476 107 846 283 213 465 931 511 632 378 594 732 942 053 291 554 519 641 861 084 701 081 135 043 648 742 081 247 169 650 980 824 359 937 460 375 243 860 549 910 565 278 335 454 952 329 848 083 353 096 239 237 389 959 263 098 234 831 832 139 223 896 341 251 478 082 772 611 627 030 798 356 337 930 215 506 087 194 224 901 166 091 100 188 464 678 604 522 172 032 294 810 342 207 269 225 002 674 386 180 154 345 829 514 234 908 836 444 020 438 335 175 453 265 053 182 443 932 474 694 815 803 283 799 465 734 979 460 310 454 816 751 416 300 950 275 207 208 963 066 740 799 248 661 317 055 264 382 949 360 712 571 626 661 026 520 510 975 817 417 654 808 336 584 166 409 476 785 225 038 811 885 , which is a lot. 3
Of course, the number above is unfair, since we already have a way of reducing the effective number of nodes by skipping dependencies. When we run the skip-dependents algorithm, we find that the average size set of nodes needed to cover the whole graph is 223. The number of possible batching arrangements of 223 nodes is 1 004 049 625 822 785 951 249 518 425 719 928 918 286 896 512 494 659 519 187 887 127 711 484 623 876 076 436 041 540 591 865 696 534 436 302 715 833 202 904 328 992 491 901 573 694 028 944 545 542 105 988 844 060 557 719 777 371 514 205 364 453 184 534 227 537 669 600 346 993 637 380 643 938 801 660 519 394 184 616 731 015 565 569 074 903 552 761 891 337 074 722 157 925 554 249 427 248 905 798 127 728 711 896 580 , which is a lot.
So, we need to find a compromise that picks good batches without waiting around to find the absolute best one.
Best partner
One compromise is to work through in an arbitrary order, but for each node we encounter, pick the best possible partner for it from the other nodes. This means in the worst case we need to evaluate (N^2)/2 unions. We will call this algorithm 'pick-best-partner'.
The code for pick-best-partner is shown in listing 10.
void algorithm_pick_best_partner( const DependencyGraph& graph, IGraphLoader& loader )
{
// This set contains nodes that have not yet been
// processed
set<Node> remaining_set = get_minimal_set(
graph );
while( !remaining_set.empty() )
{
// This set is what we will load
set<Node> current_set;
for( set<Node>::iterator it =
remaining_set.begin();
it != remaining_set.end(); )
{
current_set.insert( *it );
remaining_set.erase( it );
it = remaining_set.end();
size_t best = loader.GetMaxNodes();
// Even our best match must be below the limit
for( set<Node>::iterator i =
remaining_set.begin();
i != remaining_set.end(); ++i )
{
set<Node> current_plus_one(
current_set );
current_plus_one.insert( *i );
size_t dep_size =
get_dependency_set_size(
current_plus_one, graph );
if ( dep_size < best )
{
best = dep_size;
it = i;
}
}
}
// Load the best set we have found.
loader.LoadNodes( current_set );
}
}
|
| Listing 10 |
The result of running this algorithm against 1000 random graphs is:
....
Percentage of failures: 0
Average number of individual node loads: 1104
Average number of load events: 3.042
Average largest load size: 398
Average batch calculation time: 2.73926 seconds
....
This algorithm produces a good result, with fewer load events being needed than for the arbitrary-batches algorithm. However, it is considerably more complex than the other algorithms, which makes it harder to understand, and it is also more computationally expensive. It is worth considering simpler alternatives.
Order by size
The last algorithm we considered is called 'order-by-size'. It is computationally simple, and produces results comparable with pick-best-partner.
The order-by-size algorithm is designed to exploit a common property of graphs, which is that they often consist of relatively separate clusters of connected nodes. As illustrated in figure 2, let us imagine that we have a cluster of nodes that is depended on by several others: A, B and C. The first thing to note is that there is no need for us explicitly to load any of the nodes in the cluster, since they will automatically be loaded when any of A, B or C is loaded. In fact, using the skip-dependents algorithm, they will all be loaded three times - once for each of A, B and C.
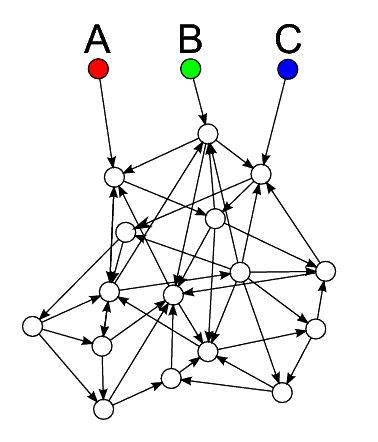
|
| Figure 2 |
It is obviously a good solution in this case for us to batch A, B and C together, and the pick-best-partner algorithm is quite likely to do this.
If we assume that our graphs are of a structure like this, however, there is a simpler algorithm that may well result in A, B and C being batched together. It comes from the observation that the set of dependencies of A, B and C are of similar size. Thus if we order the nodes by the size of their dependency set, and then perform the same algorithm as arbitrary-batches, we are likely to place A, B and C near each other in our ordering, and therefore to batch them together. This algorithm is much less complex and computationally expensive than pick-best-partner so if it works well, it may be more helpful when we have very large graphs.
The code for order-by-size is shown in listing 11.
typedef pair<size_t, Node> size_node_pair;
struct NodeToPair
{
NodeToPair( const DependencyGraph& graph )
: graph_( graph )
{
}
/** Given a node, returns a pair of the size of
* its dependency set and the node. */
size_node_pair operator()( const Node& v )
{
set<Node> tmp_set;
tmp_set.insert( v );
return size_node_pair(
get_dependency_set_size( tmp_set,
graph_ ), v );
}
const DependencyGraph& graph_;
};
void algorithm_order_by_size( const DependencyGraph& graph, IGraphLoader& loader )
{
set<Node> minimal_set = get_minimal_set(
graph );
// Create a set of nodes sorted by their
// dependency set size.
NodeToPair v2p( graph );
// Create a converter v->(size,v)
set<size_node_pair> sorted_set;
transform( minimal_set.begin(),
minimal_set.end(),
inserter( sorted_set, sorted_set.begin() ),
v2p );
// The rest is identical to arbitrary-batches,
// except looping through sorted_set instead of
// minimal_set.
set<Node> current_set;
set<Node> proposed_set;
for( set<size_node_pair>::const_iterator ssit =
sorted_set.begin();
ssit != sorted_set.end(); ++ssit )
{
proposed_set.insert( ssit->second );
if( proposed_set.size() > 1 &&
get_dependency_set_size( proposed_set,
graph ) > loader.GetMaxNodes() )
{
loader.LoadNodes( current_set );
proposed_set.clear();
proposed_set.insert( ssit->second );
current_set.clear();
}
current_set.insert( ssit->second );
}
if( !current_set.empty() )
{
loader.LoadNodes( current_set );
}
}
|
| Listing 11 |
The result of running this algorithm against 1000 random graphs is:
....
Percentage of failures: 0
Average number of individual node loads: 1104
Average number of load events: 3.008
Average largest load size: 397
Average batch calculation time: 0.056774 seconds
....
This algorithm performs almost exactly as well as pick-best-partner on the random graphs against which it was tested, and is easier to understand and faster to run.
Conclusions
After our investigation, the order-by-size algorithm was chosen by our team to choose the batches of nodes to be processed in a scalable way. The next release of our product is out soon, and scales much better than the previous one.
I hope that this glimpse into the thinking process we went through as we worked to make our product scale to handle larger models provides an insight into the different ways of thinking about algorithms that are needed to address a problem in a scalable way.
I feel that our results show that sometimes the most mathematically complete algorithm can be overkill, and a much simpler approach can be a better solution. We chose a solution that satisfied our requirements, executed quickly, and avoided introducing undue complexity into the code base.
Acknowledgements
Thanks to Charles Bailey, Edmund Stephen-Smith, Ric Parkin and the reviewers for comments, correction and code.
References
[BGL] http://www.boost.org/doc/libs/release/libs/graph/
[Knuth] Knuth, Donald E. 'Combinatorial Algorithms', in preparation. Downloadable from http://www-cs-faculty.stanford.edu/~knuth/taocp.html
1 Note that if this were not the case we would need to revisit the requirement that it does not make sense for A to be in memory without B. In our case removing this constraint would be difficult since it would mean re-writing a large piece of functionality that is currently provided by a third-party component.
2 In practice, this algorithm does not necessarily perform well because it uses a lot of memory, and under certain conditions this may cause the operating system to page memory in and out from its virtual memory store, which can be extremely slow. We will not consider such practical considerations in this article: we already know that we need to limit memory usage - reducing paging would essentially mean we needed to limit it at a lower level.
3 The number of ways of partitioning different size sets are called Bell numbers. There is lots of interesting discussion of them in [ Knuth ]. The numbers shown here were calculated using a small Ruby program found on Wikipedia at http://en.wikipedia.org/wiki/Bell_number
| Copyright |
|
© Copyright International Business Machines Corporation 2010 Licensed Materials - Property of IBM This sample program may be used, executed, copied and modified without obligation to make any royalty payment, as follows: (a) for the user's own instruction and study. No other rights under copyright are granted without prior written permission of International Business Machines Corporation. NO WARRANTY These materials contain sample application programs which illustrate programming techniques. These materials and samples have not been thoroughly tested under all conditions. IBM, therefore, cannot and does not guarantee, warrant or imply the reliability, serviceability, or function of these programs. To the fullest extent permitted by applicable law, these programs are provided by IBM "AS IS", without warranty of any kind (express or implied) including any implied warranty of merchantability or fitness for particular purpose. |











