Seweryn Habdank-Wojewódzki and Janusz Rybarski present a C++ library for users of Kohonen Neural Networks.
Introduction
This article is about the Kohonen Neural Network Library written to support the implementation of Kohonen Neural Networks. The Kohonen Neural Network Library (KNNL) is written in C++ and makes extensive use of C++ language features supporting functional and generative programming styles. The library is available from http://knnl.sourceforge.net under Open Source BSD Licence [ KNNL ].
Artificial Neural Networks (Neural Networks for short) are designed to mimic the biological structure of the natural neurons in the human brain. The structure of a single artificial neuron is similar to the biological one, too. One important feature is that an artificial network can be trained in much the same way as a biological one. We can easily imagine, that some mental abilities of animals can be duplicated in the computer system e.g. classification, generalisation and prediction. Artificial Neural Networks have a wide variety of applications. They are used, for example, in speech and image recognition, signal processing (filtering, compression), data mining and classification (e.g. classification of projects, analysis of customer demand, tracking the habits of clients), knowledge discovery (recognition of different diseases from various diagnoses), forecasting (e.g. prediction of the sale rate or object trajectories), adaptive control, risk management, data validation and diagnostics of complex systems.
Kohonen Neural Networks are not the only type of Artificial Neural Networks - there are three basic kinds: Kohonen Network, Feedforward and Recurrent (of which the Hopfield Network is a particularly interesting example) [ Wiki ]. There are no precise rules to determine which kind of network to use for a given task; rather it is a matter of deep analysis to find the right one - sometimes a mixture of them is used. More important is what kind of training procedure we can use. The Kohonen Neural Network is tuned using an unsupervised training algorithm, so for that reason it is also called a Self-Organizing Map (SOM).
Other types of neural networks are tuned using supervised training algorithms. Supervised training sometimes is called training with teacher, because we compare output values from network with with a value which we expected that should be in the output (we are teachers). The comparison generally is created by calculation difference of the output value and given one. After that weights are modified with respect to calculated difference. Unsupervised training has no teacher, there are no comparisons. Training algorithms and network are prepared to modify parameters without external decisions what is proper - network is self-trained (self-organized).
Some example uses
Kohonen Networks are used mainly for classification, compression, pattern recognition and diagnostics. Here we want to offer some simple but quite different examples where the Kohonen Network can be used.
Let's consider a shop with electronic shopping carts. The neural network can recognize all carts and what each customer has in his or her cart. After recognition, we can observe representative carts - in reality, what a typical Mr. "X" bought. But the network is more flexible than the statistics, because it can divide clients into groups: women will probably have different purchases to men, and young people will have different purchases to older ones, the same between single and married people, and so on. Everyone knows how valuable this information is. If our aim is to help the customer shop quickly, the manager will place products from a particular group close to each other; or if our target is to sell everything from stock, we can place all elements from a recognised group in different parts of the shop and in the paths between those products we can place things that are expensive or hard to sell.
The next example is how it can be used for compression. Let's assume that we can lose information, so if there is a huge amount of data we can use it to train a network, and from the network we identify the most important information about data. In compressed storage we can put just the most important information. For this usage it is important that the number of recognised details is chosen to determined the length of the output independently of the length of the input. This fact can be sometimes very useful.
Let say that we need to have an intelligent spell-checker. We can train a Kohonen network using all properly written words. After training we can put there a word which is written incorrectly, and the network can say which word is the closest one, and what are further opportunities.
Classification is similar to pattern recognition, but the important work of the network is done after training. We train network using some data - this data can define classes (groups). After training we put new data as the input of the network, and we have answer to which group belongs new item.
Diagnosis is a combination of the pattern recognition and classification. But the core of the system is to define diagnostic rules (see sidebar) in the system using Kohonen Network. The sketch of the diagnostic system is that we train the network more or less manually. We define internal parameters in neural network to fit to different let's say diseases. Parameters can be the same as are typically when we control health in hospital. Then we put to the network data of other patient, and we can observe what is a hypothesis of his disease. Another possibility is that we describe the state of the patient then train the network with some data. After training we probe the network, and notice where are placed typical situations. Then we put data from a new patient and we can have hypothesis of his own state.
| Rules |
|
A simple rule would be: Patient has high level of the fat in the blood => Patient has coronary attack. A more complex rule would take more objects, so we can add that patient is a smoker, and his live is nervous and so on. In addition to conditions we can add consequences - such as a cerebral haemorrhage. So the new example is: Patient has high level of the fat in the blood, patient is smoker => Patient has coronary attack, patient has cerebral haemorrhage. The Kohonen Neural Network Library is fully equipped for examples like above - rules that can be described in numerical way as a vectors of numbers. It provides the implementation for some simple examples. For more complex examples the user may have to specialize templates for appropriate data structures, or add dedicated distance (maybe both). For details how to describe rules in the system we suggest to look in the books of Diagnostics Fuzzy Logic and Artificial Intelligence [ Korbicz03 ][ Yager94 ][ Lin96 ]. |
As an example of advance medicine application of the Kohonen network is used for image segmentation of the scans from the magnetic resonance [ Reyes-Aldasoro ]. The target in this example is to separate on the image cranium, cerebrum and other parts of human head.
A Kohonen network has been used to solve the Travelling Salesman Problem (TSP) [ Brocki ]. In this work the author assumes that every neuron represents single place that salesman visits. And then dedicated definitions, of the tasks and proper training of the networks, lead him to solutions which are quite good. Similar work is presented on the web page www.patol.com/java/TSP [ TSP ].
Generally Kohonen Neural Network is known as one of the algorithms for Data Mining and Knowledge Discovery in Data. Knowledge Discovery is very difficult task, but it is possible to use Kohonen Network for this purpose. The most important thing is to properly define the structure of the rules, which can be stored in the system, and then our data have to fit to this construction, so training will try to find in the system some rules which are satisfies.
Mathematical fundamentals of Kohonen Neural Networks
Kohonen Neural Networks are built from neurons which are placed in an organized structure. Thus:
KNN = container + neurons
The Kohonen neuron is defined as the composition of an activation function and a distance function, as shown in Figure 1.
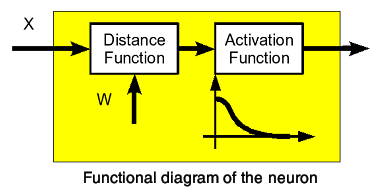
|
| Figure 1 |
The distance function (see sidebar "Distance") computes the distance between the input, X , and the neuron's internal weight, W .
| Distance |
|
In general case the are many kinds of sets where we can introduce distance. First very easy example is that we have a plane and we can measure distance between two points. Other possible example is, that we have a map of the surface of the earth and we have cities. Then we can assume that the distance is a minimal price which we have to pay to go from one city to another (we do not consider the mode of transport - it can vary, only the price). Other example of the distance can be considered in the dictionary. Let's consider such a situation. We have a set of words and we want to introduce a distance in this set. For example: the word "something" and its miskeyed versions: "somethinf", "sqmthing" and "smthng". Our intuition can say that "somethinf" is closer to correct version than word "smthng". So we can define distance in dictionary e.g. Levenshtein distance [ Levenshtein ]. The Kohonen network can work using such a distances if there will be a need. |
In this paper, the input, X, and the weight, W, can be numbers, can be vectors on the plane, or on the 3D space, or in higher dimensional space. In that particular case the weights W belong to the same space as the input values X . We can calculate the distance between X and W using Euclidean formula (see sidebar "Euclidean formula").
| Euclidean Formulas |
|
Let's assume that: X = [ x 1 , x 2 , ..., x n ] W = [ w 1 , w 2 , ..., w n ] Euclidean distance: d( X , W ) = sqrt ( (x 1 - w 1 ) 2 + ... + (x n - w n ) 2 ) Sometimes is very useful to calculate weighted Euclidean distance, so let's assume that P = [p 1 , p 2 , ..., p n ] are parameters: d P ( X , W ) = sqrt ( p 1 (x 1 - w 1 ) 2 + ... + p n (xn - wn) 2 ) |
In this article we will focus that particular distance function - it means on the Euclidean distance function. The activation function is the Gauss function (half of the full curve as shown in Figure 1.). The activation function controls the level of the output.
G (s,p) ( x ) = exp ( - 0.5 (x/s) p )
As with all neural networks, a Kohonen network is useless until it has been trained but, once trained, it is a very useful and intelligent mathematical object. It is useful because it can be applied in various branches of industry and science. It is intelligent because it can be trained without teacher - it can find some aspects in the data, that are not exposed.
Kohonen neural network must be trained. There are two main algorithms: one is called Winner Takes All (WTA), and the second is called Winner Takes Most (WTM). Details of these algorithms are described in section Training Process in this paper. Respectively to the training algorithm this structure can be either just a container (for WTA algorithm) for neurons or container equipped with distance function or topology (for WTM algorithm) - typically it is a two dimensional matrix. More generally, the network topology can be a graph or a multidimensional matrix. In medicine, especially, a 3D network topology is used for 3D image pattern recognition. In this paper the authors concentrate on the two dimensional case.
Code construction for the Kohonen Neural Network
In the library presented here we use vector < vector < T > > as a 2D matrix rather than the matrix template from the Boost uBLAS library [ Boost ]. This is because boost::matrix requires the value type to be DefaultConstructible and the neuron types in the library do not satisfy this requirement. We have suggested that the boost::matrix maintainers should add a suitable constructor to the matrix classes, so in the next version of the KNN library, the boost::matrix class will be used as a container to keep the network structure. This version of the library is restricted to 2D matrices. If need be, we will extend the structure of the network to 3D structures and graphs.
From a designer's point of view we can either construct a structure based on classes containing pointers to functions and functors (the latter being a class with declared and defined operator() ) or build up template classes that store functors by value and provide an opportunity to parametrize the code by means of policy classes. We have decided to use templates, because many errors can be detected at compilation time, so the cost of testing and debugging the program is reduced to a minimum. Moreover template functors are quite small and such a construction is modular. Imagine how many different types of networks and training algorithms we are able to store in memory and use, and be sure that they will work, as they are fully constructed at compile time.
In the previous section the structure of the Kohonen neuron was described. Now we shall show how those neurons are represented in code. We use a class template, Basic_neuron , as shown in Listing 1. The template has two parameters: the type of the distance function and the type of the activation function. It is important that a neuron cannot be default constructed. This requirement is enforced by only providing a non-default constructor. So in the construction of a neuron there is no possibility of making errors, because the neuron will work if the constructor parameter classes work.
template
<
typename Activation_function_type,
typename Binary_operation_type
>
class Basic_neuron
{
public:
/** Weights type. */
typedef typename Binary_operation_type
::value_type weights_type;
/** Activation function type. */
typedef Activation_function_type
activation_function_type;
/** Binary operation type. */
typedef Binary_operation_type
binary_operation_type;
typedef typename Binary_operation_type
::value_type value_type;
typedef typename Activation_function_type
::result_type result_type;
/** Activation function functor. */
Activation_function_type activation_function;
/** Weak and generalized distance function. */
Binary_operation_type binary_operation;
/** Weights. */
weights_type weights;
Basic_neuron
(
const weights_type & weights_,
const Activation_function_type &
activation_function_,
const Binary_operation_type & binary_operation_
)
: activation_function ( activation_function_ ),
binary_operation ( binary_operation_ ),
weights ( weights_ )
{}
const typename Activation_function_type
::result_type
operator() ( const value_type & x ) const
{
// calculate output of the neuron as activation
// function working on results from binary
// operation on weights and value.
// composition of activation and distance
// function
return activation_function ( binary_operation (
weights, x ) );
}
protected:
Basic_neuron();
};
|
| Listing 1 |
We can easily see that the Basic_neuron class does not define anything more than a composition of functors similar to the compose_f_gx_hy_t in [ Josuttis99 ]. The class stores functors by value, so as we mentioned earlier there are no pointers in that construction [ Vandevoorde03 ].
The next thing to do is to design the code for the activation function. Activation function is a concept; we could easily use e.g. the Cauchy hat function or the Gauss hat function as an activation function. The Cauchy hat function is a generalisation of the Cauchy distribution function. The integral of the Cauchy distribution function over its whole domain is 1; this is not true, in general, for the Cauchy hat function.
C (s,p) ( x ) = 1 / ( 1 + (x/s) p )
The same is true for the Gauss hat function. An outline of the code for the Gauss hat functor is shown in Listing 2; the Cauchy hat functor is similar except for the formula that calculates the outputs.
template
<
typename Value_type,
typename Scalar_type,
typename Exponent_type
>
class Gauss_function
: public Basic_function < Value_type >,
public Basic_activation_function
<
typename operators::Max_type < Scalar_type,
Exponent_type >::type,
Value_type,
typename operators::Max_type
<
typename operators::Max_type
<
typename operators::Max_type < Scalar_type,
Exponent_type >::type,
Value_type
>::type,
double
>::type
>
{
public:
typedef Scalar_type scalar_type;
typedef Exponent_type exponent_type;
typedef Value_type value_type;
typedef typename operators::Max_type
<
typename operators::Max_type
<
typename operators::Max_type < Scalar_type,
Exponent_type >::type,
Value_type
>::type,
double
>::type result_type;
/** Sigma coefficient in the function. */
Scalar_type sigma;
/** Exponential factor. */
Exponent_type exponent;
Gauss_function ( const Scalar_type & sigma_,
const Exponent_type & exp_ )
: sigma ( sigma_ ), exponent ( exp_ )
{}
const result_type operator() (
const Value_type & value ) const
{
operators::power < result_type,
Exponent_type > power_v;
// calculate result
return
(
std::exp
(
- operators::inverse (
static_cast < Scalar_type > ( 2 ) )
* (power_v)
(
operators::inverse ( sigma ) * value,
exponent
)
)
);
}
};
|
| Listing 2 |
We use a class template with three type parameters. Value_type is the type of the value that will be passed to the function. Scalar_type is the type of the scaling factor, and Exponent_type is the type of the exponent. All parameters are important, because generally Value_type and Scalar_type are some sort of floating point type like double or long double, and Exponent_type is used to choose the most appropriate power algorithm. This is important, because we won't always use the floating point power operation; sometimes we can use the faster and more accurate power function for integral exponents. So the library defines two specialisations of the power functor: one for integral exponents, and one based on the std::pow calculation for floating point exponents.
The library uses two coding tricks derived from modern C++ software design. The first one we call Grouping Classes. This technique is used to ensure that the class templates are only instantiated with the correct template parameters.
In our library we have a lot of functors. They all define operator() . When we write code it would be easy to use the wrong functor as a parameter of a class template. We might try to solve this problem by putting related functors into separate namespaces, e.g. we might require that foo::Foo is only parametrized by functors from namespace foo . But this is just a hint to the programmer; it can not be checked by the compiler. There is also the problem of how to set up namespaces if there are some functors that could parametrize both class bar::Bar and foo::Foo . Multiple inheritance helps here. If we have a set of functors and some of them are only valid as parameters to bar::Bar , some are only valid as parameters to foo::Foo , and the rest will fit both templates, we could define two empty classes with name e.g. Fit_to_Foo and Fit_to_Bar, and all functors derive from them with respect to the represented traits. Sample code could be like Listing 3.
#include <boost/static_assert.hpp>
#include <boost/type_traits.hpp>
// helpful template
template<typename T, typename Group>
struct is_in_group {
enum {value = boost::is_base_of<Group,T>::value };
};
// define groups
struct Fit_to_Foo {};
struct Fit_to_Bar {};
// set functors as a member of group
class Functor_A : public Fit_to_Foo { ... };
class Functor_B : public Fit_to_Bar { ... };
class Functor_C : public Fit_to_Bar,
public Fit_to_Foo { ... };
// example template classes that check if parameter
// is in proper group
template < typename T >
class Any_class_that_accepts_functors_only_from_Foo_group
{
// and for example in constructor we can put:
BOOST_STATIC_ASSERT(
( is_in_group < T, Fit_to_Foo >::value ) );
};
|
| Listing 3 |
The BOOST_STATIC_ASSERT macro will generate a compiler error if T is not derived from Fit_to_Foo . So there is a compile-time check that the programmer has used a valid functor as a template parameter. Even though all the functor classes define operator() , they will not all fit our template. And the static assertion has no run-time overhead because it doesn't generate any code or data.
In KNNL this technique is used for hat functions. The Gauss hat function will be used as the activation function and later as a helper function in the training algorithms. But this function is not valid for other purposes, so we derive Gauss_function from Basic_function and from Basic_activation_function . In template classes which will use them we could check which classes they are derived from using boost::is_base_of . If we use BOOST_STATIC_ASSERT or BOOST_MPL_ASSERT_MSG we can check if the hat function class is derived from the appropriate base, which guarantees that some minimal functionality is available and the class models the correct concept [ Abrahams04 ]. If we don't do this and we use as a parameter any class that fits the type requirements, the template will compile, but the parameter (functor) may not meet the semantic requirements of the template. This technique is an extension of the concept traits technique, because in concept traits we are sure only that the class contains the necessary methods; but if we ensure that it is derived from Basic_activation_function it is guaranteed to be a valid activation function. The authors call this technique Grouping Classes although there is no name in the literature for this coding style as there is for type traits or concept traits [ Traits ]. At this stage of the work the code does not include such checks; this will be added in the next version of the library after feedback from users. The rest of the Gauss_function class uses the power and inverse functors, which implement the common mathematical functions x y and 1/x, to generate the proper results.
Another important feature of the library is the metafunction shown in Listing 4 ( Max_type < Scalar_type, Exponent_type > ).
template < typename S, typename T >
struct Max_type_private
{};
template < typename T >
struct Max_type_private < T, T >
{
typedef T type;
};
#define MAX_TYPE_3(T1,T2,T3) template <>\
struct Max_type_private < T1, T2 >\
{ typedef T3 type; };
MAX_TYPE_3(int,double,double)
MAX_TYPE_3(short,long,long)
MAX_TYPE_3(unsigned long,double,double)
// an example where we can explicitly use three
// different types MAX_TYPE(std::complex < int >,
// double, std::complex < double >)
// macro below assumes that bigger type is the
// first one
// macro MAX_TYPE_2( argument_1_type,
// argument_2_type )
// simulate default result_type that result_type
// = argument_1_type
#define MAX_TYPE_2(T1,T2) template <>\
struct Max_type_private < T1, T2 >\
{ typedef T1 type; };
MAX_TYPE_2(double,int)
MAX_TYPE_2(long,short)
MAX_TYPE_2(double,unsigned char)
MAX_TYPE_2(double,unsigned long)
template
<
typename T_1,
typename T_2
>
class Max_type
{
private:
typedef typename boost::
remove_all_extents < T_1 >::type T_1_t;
typedef typename boost::
remove_all_extents < T_2 >::type T_2_t;
public:
typedef typename Max_type_private < T_1_t,
T_2_t >::type type;
};
|
| Listing 4 |
The goal of this metafunction is to return a type that can represent any value on types T_1 and T_2 . This template is used to deduce the output type of functors from their input values types (presented here the number of the propositions of the usage of MAX_TYPE_2 and MAX_TYPE_3 is reduced - there are more examples in the library ) .
The last part of the neuron is the distance function which is designed to work for any container. The Euclidean distance function, which is easy to understand, is presented in Listing 5 - the library also provides the weighted Euclidean distance function. To avoid problems (e.g. lost of performance) with the square root function, the functor actually returns the square of the Euclidean distance (we omit calculation of the square root function). If the user needs the real Euclidean distance from this functor he/she should either calculate the square root from this value, or set the proper exponent in activation function.
template
<
typename Value_type
>
class Euclidean_distance_function
: public Basic_weak_distance_function
<
Value_type,
Value_type
>
{
public:
const typename Value_type::value_type operator()
(
const Value_type & x,
const Value_type & y
) const
{
return
(
euclidean_distance_square
(
x.begin(),
x.end(),
y.begin(),
static_cast < const typename Value_type
::value_type & > ( 0 )
)
);
}
private:
typedef typename Value_type
::value_type inner_type;
const inner_type euclidean_distance_square
(
typename Value_type::const_iterator begin_1,
typename Value_type::const_iterator end_1,
typename Value_type::const_iterator begin_2,
const inner_type & init
) const
{
return std::inner_product
(
begin_1, end_1, begin_2,
static_cast < inner_type > ( init ),
std::plus < inner_type >(),
operators::compose_f_gxy_gxy
(
std::multiplies < inner_type >(),
std::minus < inner_type >()
)
);
}
};
|
| Listing 5 |
This function will be used as the binary_operation in neuron construction. The Euclidean_distance_function template is designed for any data stored in any container as defined in the C++ Standard Library. User-defined value types can be used with the Euclidean distance function provided the mathematical operations of addition, subtraction and multiplication are defined on them and the identity element under addition is formed by construction from the integer value 0.
Listing 6 shows the complete code for a Kohonen network. Here, R is the number of rows in the network matrix, C is the number of columns, g_a_f is the chosen activation function, e_d is the chosen distance function, data is a data set of type vector < V_d > , kohonen_network is the network to be initialized and IR is a policy class for configuring the random number generator. (Random number generation is important for the implementation but it is too detailed for this short paper. Further explanation is included in the reference manual). Data are used just for setting up ranges in data space. In generation process ranges are used for randomly generated weights in network (uniformly in data space with respect to the ranges of the data). There are several algorithms for initialising the neuron weights. In this library the weights are assigned random values between the minimum and maximum values in the input data. So, for example, if the input data are:
{ (1,-2,-1), (-1,3,-2), (2,1,0), (0,0,1) }
the weights will be assigned random values in the range (-1,-2,-2) through (2,3,1). This completes the code to create and generate the weights of the Kohonen Neural Network. As we can see our desire for flexible code is fulfilled, even though we are not using pointers.
// type of the single data vector
// for example if we have tuples of the data like:
// {(1,2,3),(2,3,4),(3,4,5),(4,5,6),(5,6,7), ... }
// this data could describe position of pixel and
// it's colour
// V_d describes type of e.g. (1,2,3)
typedef vector < double > V_d;
// configure Gauss hat function
typedef neural_net::Gauss_function
< double, double, int > G_a_f;
// Activation function for the neurons with some
// parameters
G_a_f g_a_f ( 2.0, 1 );
// prepare Euclidean distance function
typedef distance::Euclidean_distance_function
< V_d > E_d_t;
E_d_t e_d;
// here Gauss activation function and Euclidean
// distance is chosen to build Kohonen_neuron
typedef neural_net::Basic_neuron
< G_a_f, E_d_t > Kohonen_neuron;
// Kohonen_neuron is used for the constructing a
// network
typedef neural_net::Rectangular_container
< Kohonen_neuron > Kohonen_network;
Kohonen_network kohonen_network;
// generate networks initialized by data
neural_net::generate_kohonen_network
//<
// vector < V_d >,
// Kohonen_network,
// neural_net::Internal_randomize
//>
( R, C, g_a_f, e_d, data, kohonen_network, IR );
|
| Listing 6 |
Training process
The training process is very important, because the untrained network has no idea why it exists. The more training passes are applied the greater the effect of the training. And after that the weights of the neurons can bring out many important properties of the data. For example, how the data can be generalized, how the data might be represented, what clusters (groups) exist in the data and so on.
There are two training algorithms for the Kohonen network. As we said in the beginning, the first is called Winner Takes All (WTA), and the second is Winner Takes Most (WTM).
WTA is very easy to understand and implement. When data is placed on the input to the neural network all the outputs are compared and the neuron with the highest response is chosen. This means that the weights of the winning neuron are quite close to the data. The winning neuron is the neuron with the highest response for the given input value. The weights for this neuron only are modified:
w(t+1) = w(t) + C(t) ( x - w(t) )
where: w(t) is the weight(s) after training pass t , w(t+1) is the modified weight(s), x is the input data, and C is a training coefficient which may vary as the training process proceeds.
Generally the behaviour of the WTA training algorithm is that it invests only in winners. Very radical method, isn't it? The WTM training process is more complicated. As in WTA we look for the best neuron, but we train all neurons in neighbourhood.
w M (t+1) = w M (t) + G( w(t), x, N, M, t )( x - w M (t) )
where: w(t) is the existing weight(s) of the trained neuron (not only the winner), w(t+1) is the modified weight(s) of this neuron, x is the input data, and G is a training function, N is neuron which is mostly activated (the winner), M denotes trained neuron.
Function G depends on the relation between the winning neuron N and the trained neuron M , also between the weight w M and the data x . The library provides some ready-made WTM algorithms, too. The WTM algorithm trains groups of neurons, as much as they fit to the data.
The 2D topologies supported by the library are: Hexagonal topology, City topology and Maximum topology. In these diagrams (Figure 2.) we can see that the same 4x4 matrix can have different topologies which define different shapes of neighbourhood (on figures are shown neighbourhoods of the radius equals 1). In the WTM algorithm the winner will be improved a lot, but the neighbours will be improved too - the effect falling off with distance in the neural network and some other parameters defined by the G function.
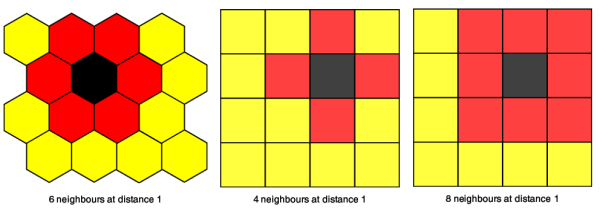
|
| Figure 2 |
Implementation of the training algorithms
To be consistent with the design of the neuron, we decide to continue using class templates. A schematic of the training process is shown on Figure 3.
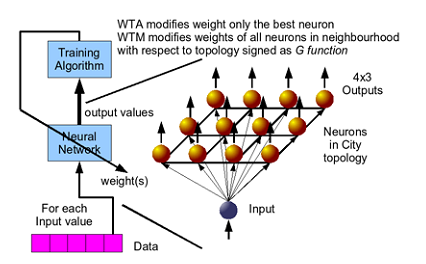
|
| Figure 3 |
The code for the WTA algorithm is shown in Listing 7.
template
<
typename Network_type,
typename Value_type,
typename Data_iterator_type,
typename Training_functional_type,
typename Numeric_iterator_type
= Linear_numeric_iterator <
typename Training_functional_type
::iteration_type
>
>
class Wta_training_algorithm
{
public:
typedef typename
Training_functional_type::iteration_type
iteration_type;
typedef Numeric_iterator_type
numeric_iterator_type;
typedef Network_type network_type;
typedef Value_type value_type;
typedef Data_iterator_type data_iterator_type;
typedef Training_functional_type
training_functional_type;
/** Training functional. */
Training_functional_type training_functional;
Wta_training_algorithm
(
const Training_functional_type &
training_functional_,
Numeric_iterator_type numeric_iterator_ =
linear_numeric_iterator()
)
: training_functional ( training_functional_ ),
numeric_iterator ( numeric_iterator_ )
{
network = static_cast < Network_type* > ( 0 );
}
const int operator()
(
Data_iterator_type data_begin,
Data_iterator_type data_end,
Network_type * network_
)
{
network = network_;
// check if pointer is not null
assert ( network != static_cast <
Network_type * > ( 0 ) );
// for each data train neural network
std::for_each
(
data_begin, data_end,
boost::bind
(
& Wta_training_algorithm
<
Network_type,
Value_type,
Data_iterator_type,
Training_functional_type,
Numeric_iterator_type
>::train,
this,
_1
)
);
return 0;
}
protected:
/** Pointer to the network. */
Network_type * network;
iteration_type iteration;
Numeric_iterator_type numeric_iterator;
void train ( const Value_type & value )
{
size_t index_1 = 0;
size_t index_2 = 0;
typename Network_type::value_type
::result_type tmp_result;
// reset max_result
typename Network_type::value_type
::result_type max_result
= std::numeric_limits
<
typename Network_type
::value_type::result_type
>::min();
typename Network_type::row_iterator r_iter;
typename Network_type::column_iterator c_iter;
// set ranges for iteration procedure
size_t r_counter = 0;
size_t c_counter = 0;
for ( r_iter = network->objects.begin();
r_iter != network->objects.end();
++r_iter
)
{
for ( c_iter = r_iter->begin();
c_iter != r_iter->end();
++c_iter
)
{
tmp_result = ( *c_iter ) ( value );
if ( tmp_result > max_result )
{
index_1 = r_counter;
index_2 = c_counter;
max_result = tmp_result;
}
++c_counter;
}
++r_counter;
c_counter = 0;
}
r_iter = network->objects.begin();
std::advance ( r_iter, index_1 );
c_iter = r_iter->begin();
std::advance ( c_iter, index_2 );
// train the winning neuron
(training_functional)
(
c_iter->weights,
value,
this->iteration
);
// increase iteration
++numeric_iterator;
iteration = numeric_iterator();
}
};
|
| Listing 7 |
The function call operator calls the private train function for each item of data. The train function finds the winning neuron and applies the training_functional to it. Listing 8 shows the code for the training_functional class template:
template
<
typename Value_type,
typename Parameters_type,
typename Iteration_type
>
class Wta_proportional_training_functional
: public Basic_wta_training_functional
<
Value_type,
Parameters_type
>
{
public:
typedef Iteration_type iteration_type;
/** Shifting parameter for linear function */
Parameters_type parameter_0;
/** Scaling parameter for linear function */
Parameters_type parameter_1;
Wta_proportional_training_functional
(
const Parameters_type & parameter_0_,
const Parameters_type & parameter_1_
)
: parameter_0 ( parameter_0_ ),
parameter_1 ( parameter_1_ )
{}
Value_type & operator()
(
Value_type & weight,
const Value_type & value,
const iteration_type & s
)
{
using namespace operators;
return
(
weight
= weight
+ ( parameter_0 + parameter_1 * s )
* ( value - weight )
);
}
};
|
| Listing 8 |
So we could go deeper and deeper defining further class templates to build up the code for all the training procedures. Listing 9 presents part of the code that brings all the pieces together, creates the WTA training algorithm and, finally, trains the network generated earlier.
// data container like:
// {(1,2,3),(2,3,4),(3,4,5),(4,5,6),(5,6,7), ... }
typedef vector < V_d > V_v_d;
// construct WTA training functional
typedef neural_net::Wta_proportional_training_functional
< V_d, double, int >
Wta_train_func;
// define proper functional and its parameters
Wta_train_func wta_train_func ( 0.2 , 0 );
// construct WTA training algorithm
typedef neural_net::Wta_training_algorithm
< Kohonen_network, V_d, V_v_d::iterator,
Wta_train_func >
Learning_algorithm;
// define training algorithm
Learning_algorithm training_alg ( wta_train_func );
// set number of the training epochs
// one epoch it is training through all data
// stored in container
const int no_epoch = 30;
// print weights before training process
neural_net::print_network_weights ( cout, kohonen_network );
// train network
for ( int i = 0; i < no_epoch; ++i )
{
training_alg ( data.begin(), data.end(),
&kohonen_network );
// better results are reached if data are sorted
// in each cycle of the training
// in target procedure this functionality
// could be prepared using
// proper policy like Shuffle_policy
std::random_shuffle ( data.begin(), data.end() );
}
// print weights after training process
neural_net::print_network_weights
( cout, kohonen_network );
|
| Listing 9 |
The code for the WTA method presented here is just an overview showing how the rest of the code is structured. WTM is much bigger and complicated, but also much more effective. Both algorithms are implemented in the library.
Usage of the network
Generally the structure e.g. topology, input and outputs of the trained network are shown in Figure 3. After training the network can be used in the same way as other neural networks. We can put the input value, and we can simply read outputs. The function below will return output value of the (i,j) -th neuron when we set the input value.
network ( i, j ) ( input_value );
or directly:
network.objects[i][j] ( input_value );
There are other useful functions for printing values and weights from network. The first one (from the print_network.hpp file) is:
print_network
The example of the usage is shown below. In the examples kohonen_network is a network and *(data.begin()) is the first value from the set of training data, but there can be used other input values, too:
neural_net::print_network ( std::cout,
kohonen_network, *(data.begin()) );
Other is for printing only weights:
print_network_weights
The example of the usage is shown below:
neural_net::print_network_weights ( std::cout,
kohonen_network );
All details are available in the reference manual, both function are just loops through the network container. The first function calculates every output value. The second one take every weight of the neuron and print it.
Interpretation of the results
One interpretation of the network is that after training we are looking on values of the weights of all neurons. The weights can be treated as "centres" of the clusters.
If we have a network with 3 neurons, and we will train it with a set of data. We can noticed that weights of the neurons will concentrate in the centres of the data groups. We do not need define any group, Kohonen network will find as many group as is number of neurons what is shown on Figure 4. Thanks to the network and training process we have generalisation of the data. After training if we put in to the network input new data (similar to shown in Figure 4.) the network will activate neurons - it mean that we can read output values, and then we can look which neuron have the highest response - we call it "winner". We can say that new data belongs to the cluster (group) which is represented by this neuron and we can read the weights of this neuron.
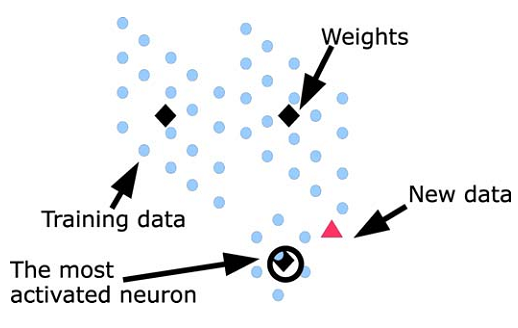
|
| Figure 4 |
This is important in all branches of the computation from business, through medicine, from signal processing e.g. image compression, to the weather prediction. Everywhere when we have a lot of data, and we do not really know what they are generally represent.
After training if we put input value to the network, we can observe responses from all neurons. Then we can say e.g. that the given input value belongs to the cluster e.g. "A" which is represented by the neuron with the highest response. Further we can say in "fuzzy" language that this particular value belongs the most to cluster e.g. "A", however it belongs to other clusters "B" and "D", but not to "C", where every cluster is represented by the single neuron.
Conclusions
In this paper we have presented the design and implementation of a Kohonen neural network library using class templates and a functional programming style. The KNNL library uses the Boost library. The training algorithms have been tested and found to produce quite good results. After implementation the library we observe that class templates are very useful for creating very flexible mathematical code.
Acknowledgements
Seweryn would like to thank Bronek Kozicki for help with the publication of this work, and Michal Rzechonek who always helps to improve my programming skills, and Phil Bass who gives many important remarks to the coding style and shape of this article. Moreover Seweryn would like to thanks Alan Griffiths for help in preparing final version of this paper more oriented to the programmers needs.
References
[ Wiki] Artificial Neural Networks , http://en.wikipedia.org/wiki/Artificial_neural_network
[ Boost] Boost::uBlas , http://www.boost.org/libs/numeric/ublas/doc/matrix.htm
[ Josuttis99] The C++ Standard Library: A Tutorial and Reference , N. M. Josuttis, Addison Wesley Professional, 1999.
[ Vandevoorde03] C++ Templates: The Complete Guide , D. Vandevoorde, N. M. Josuttis, Addison Wesley Professional, 2003.
[ Abrahams04] C++ Template Metaprogramming: Concepts, Tools, and Techniques from C++ Boost and Beyond , D. Abrahams, A. Gurtovoy, Addison Wesley, 2004.
[ Traits] Concept Traits , http://www.neoscientists.org/~tschwinger/boostdev/concept_traits/libs/concept_traits/doc/
[ Reyes-Aldasoro] Image Segmentation with Kohonen Neural Network Self-Organizing Map , Contsantino Carlos Reyes-Aldasoro, http://www.cs.jhu.edu/~cis/cista/446/papers/SegmentationWithSOM.pdf
[ Brocki] Kohonen Self-Organizing Map for the Traveling Salesperson Problem , Lukas Brocki, http://www.tokyolectures.pjwstk.edu.pl/files/lucas_tsp.pdf
[ TSP] Travelling Salesman Problem , http://www.patol.com/java/TSP/
[ KNNL] Source code of the KNNL , http://knnl.sourceforge.net
[ Levenshtein] Levenshtein Distance , http://www.merriampark.com/ld.htm#WHATIS
[ Korbicz03] Fault Diagnosis: Models, Artificial Intelligence, Applications , J. Korbicz, Springer-Verlag, 2003.
[ Yager94] Essential of Fuzzy Modelling and Control , R. R. Yager, D. P. Filev, John Willey & Sons, 1994.
[ Lin96] Neural Fuzzy System - A Neuro-Fuzzy Synergism to Intelligent Systems , C.-T. Lin, C. S. G. Lee, Prentice-Hall, 1996.











